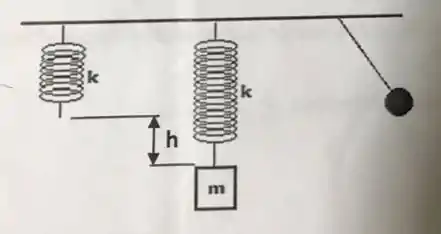
II – A figura abaixo mostra que, se pendurarmos um bloco na extremidade de uma mola de constante elástica k, a mola sofrerá um alongamento h = 4 cm. Se puxarmos o bloco ligeiramente para baixo a partir da posição de equilíbrio e depois liberarmos, ele oscilará com certa frequência. Qual deve ser o comprimento de um pêndulo simples para que oscile com a mesma frequência?
Passo 1
Fazendo o equilíbrio de forças nesse bloquinho, podemos escrever:
Então:
Vou escrever de outra forma:
Trocando os valores de g e h:
E aí vamos relembrar que a frequência angular é:
No sistema massa mola. E no pêndulo simples:
Igualando os dois:
Trocando o valor que nós encontramos para k/m:
Resposta
0,04 m
Exercícios de Livros Relacionados
Suponha que um pêndulo simples é formado por um pequeno peso de 60,0 g pendurado na extremidade de uma corda de massa desprezível. Se o ângulo θ entre a corda e a vertical é dado por θ = 0,0800rad cos
Uma artista de circo, sentada em um trapézio, está balançando com um período de 8,85 s . Quando fica de pé, elevando assim de 35,0 c m o centro de massa do sistema t r a p é z i o + t r a p e z i s t
Mostre que a energia total de um pêndulo simples sob oscilações de pequena amplitude ϕ 0 (em radianos) é E ≈ 1 2 m g L ϕ 0 2 . Dica: Use a aproximação c o s ϕ ≈ 1 - 1 2 ϕ 2 para pequenosϕ .
No Planeta X , onde o valor de g é desconhecido, um pêndulo oscila com período T = 2s . Qual será o período deste pêndulo se: a. Sua massa for duplicada? Explique. Note que você não sabe quais são os
Na figura, uma mola de demolição de 2500k g balança na ponta de um guindaste. O comprimento do segmento de cabo que se move com a bola é 17m . (a) Determine o período do balanço, supondo que o sistema