O pêndulo da figura abaixo é formado por uma haste rígida de massa desprezível, com uma bola de massa em sua extremidade. A bola na extremidade do pêndulo descreve um arco de círculo de raio que atinge a sua altura máxima no ponto B.
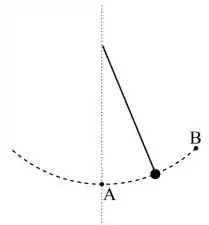
Sobre o movimento do pêndulo, escolha a alternativa correta:
(A) A velocidade da bola é nula no ponto A.
(B) A aceleração da bola é nula no ponto B.
(C) A velocidade da bola é nula no ponto B.
(D) Em toda a trajetória, a aceleração da bola aponta para o centro do círculo.
(E) Em toda a trajetória, a aceleração da bola aponta verticalmente para baixo.
Passo 1
(A) A velocidade da bola é nula no ponto A.
A velocidade do pêndulo no ponto A é máxima, pois esse é o ponto mais baixo da sua trajetória.
A afirmativa (A) está incorreta.
Passo 2
(B) A aceleração da bola é nula no ponto B.
O ponto B é o ponto de maior altura que o pêndulo alcança. Assim, o pêndulo tem velocidade igual a zero, para trocar o sentido do movimento e passar a descer novamente.
Por mais que a velocidade seja nula, a aceleração não é!
Existe uma força resultante na bola que gera uma aceleração na mesma:
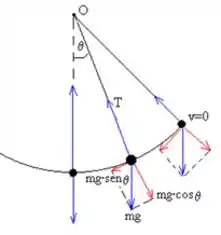
A afirmativa (B) está incorreta.
Passo 3
(C) A velocidade da bola é nula no ponto B.
Realmente a velocidade no ponto B é nula! Assim como falamos no PASSO 2, o ponto B é o ponto de altura máxima, ou seja, maior amplitude/abertura do pêndulo.
Logo, a bola chega ao ponto B com velocidade nula e passa a ganhar velocidade no sentido oposto.
A afirmativa (C) está correta e ficamos com essa para nossa resposta.
Vamos dar uma olhadinha nas outras mesmo assim...
Passo 4
(D) Em toda a trajetória, a aceleração da bola aponta para o centro do círculo.
(E) Em toda a trajetória, a aceleração da bola aponta verticalmente para baixo.
Ambas estão erradas pois a aceleração da bola vai mudando de direção ao longo do movimento.
Olhando para essa figura, podemos ver as forças sobre a bola:
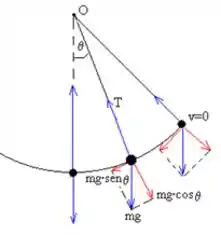
A força de tração sempre atua na direção radial, enquanto a força peso (aponta para baixo) tem uma componente na direção radial e outra na direção tangencial (em vermelho).
A força resultante na direção radial (apontando para o centro) resulta numa componente da aceleração nessa direção (aceleração centrípeta).
Enquanto a componente da força peso na direção tangencial gera uma aceleração nessa direção (exceto no ponto mais baixo).
Logo, a aceleração sofrida pela bolinha tem uma componente radial e uma componente tangencial ao longo do movimento, com exceção do ponto mais baixo onde a aceleração está apenas na direção radial.
As afirmativas (D) e (E) estão incorretas.
Resposta
Letra (C)