A Figura mostra um pêndulo de comprimento com uma bolinha de massa . A bolinha é presa a uma mola de constante de força , como mostrado. Quando a bolinha está diretamente abaixo do suporte do pêndulo, a mola está frouxa.
Seja o ângulo entre a haste a vertical. Para muito pequeno:
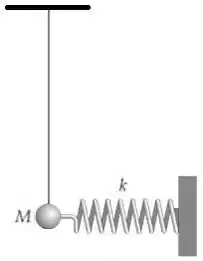
Calcule o período do pendulo.
Passo 1
Bom, vamos lá...Vamos começar fazendo um esboço de diagrama de corpo livre para identificarmos as forças que agem no sistema.
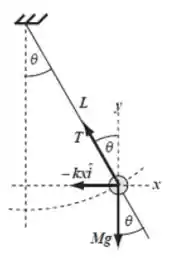
Pela figura, vemos que as forças que agem na direção horizontal são:
Quanto vale a tensão? Podemos descobrir isso fazendo o equilíbrio vertical das forças:
Assim, na primeira equação:
Como para pequenos ângulos:
E do enunciado:
E:
Assim:
Passo 2
Opa! Essa é uma EDO no formato que nós conhecemos! Looogo,
Resposta
Exercícios de Livros Relacionados
Suponha que um pêndulo simples é formado por um pequeno peso de 60,0 g pendurado na extremidade de uma corda de massa desprezível. Se o ângulo θ entre a corda e a vertical é dado por θ = 0,0800rad cos
Uma artista de circo, sentada em um trapézio, está balançando com um período de 8,85 s . Quando fica de pé, elevando assim de 35,0 c m o centro de massa do sistema t r a p é z i o + t r a p e z i s t
Mostre que a energia total de um pêndulo simples sob oscilações de pequena amplitude ϕ 0 (em radianos) é E ≈ 1 2 m g L ϕ 0 2 . Dica: Use a aproximação c o s ϕ ≈ 1 - 1 2 ϕ 2 para pequenosϕ .
No Planeta X , onde o valor de g é desconhecido, um pêndulo oscila com período T = 2s . Qual será o período deste pêndulo se: a. Sua massa for duplicada? Explique. Note que você não sabe quais são os
Na figura, uma mola de demolição de 2500k g balança na ponta de um guindaste. O comprimento do segmento de cabo que se move com a bola é 17m . (a) Determine o período do balanço, supondo que o sistema