Origem do Exercício
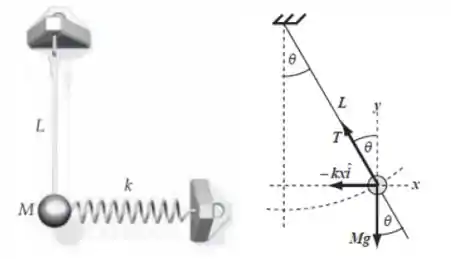
A Figura mostra um pêndulo de comprimento com uma bolinha de massa . A bolinha é presa a uma mola de constante de força , como mostrado. Quando a bolinha está diretamente abaixo do suporte do pêndulo, a mola está frouxa.
a)Seja o ângulo entre a haste a vertical. Para pequeno temos que onde .Calcule o período do pendulo em função de .
b)O diagrama de forças é apresentado na figura ao lado. Calcule em função . Assuma que
c)A partir do resultado anterior obtenha o período do pendulo se .
Dados: Para muito pequeno:
Passo 1
a)
A equação que temos é a:
Sabendo que:
Temos:
Que é uma EDO no formato que nós conhecemos. Assim:
Passo 2
b):
Pela figura, vemos que as forças que agem na direção horizontal são:
Quanto vale a tensão? Podemos descobrir isso fazendo o equilíbrio vertical das forças:
Assim, na primeira equação:
Como para pequenos ângulos:
E do enunciado:
E:
Assim:
Assim:
Passo 3
c)
Se
Substituindo na expressão do período antes calculada:
Resposta
a)
b)
c)