
Passo 1
a)
Primeiramente é pedido o diagrama de forças sobre a bala enquanto esta penetra a madeira:
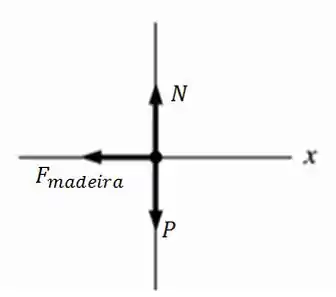
Aqui temos:
N: Força normal
P: Força peso
: Força de resistência da madeira
Passo 2
b)
Aqui vamos aplicar primeiramente a equação da cinemática para descobrirmos a desaceleração que a bala tem enquanto entra na parede. Depois, vamos achar a força resistiva da madeira por meio da Segunda Lei de Newton, que relaciona essa força resistiva em x com a aceleração em x.
Então, vamos lá!
Aplicando:
Sabemos que , e . Resolvendo:
Passo 3
b)
Seguindo a linha do raciocínio explicado no passo anterior, vamos usar a Segunda Lei de Newton agora:
Vemos pelo diagrama de forças que a força resultante em x é justamente a força resistiva da madeira.
Assim:
Passo 4
c)
Para achar o tempo de parada, vamos recorrer novamente à cinemática:
Sabemos que , e :
Passo 5
d)
Agora é pedido um gráfico da velocidade vs tempo da bala dentro da madeira.
Basta usarmos a equação do passo anterior:
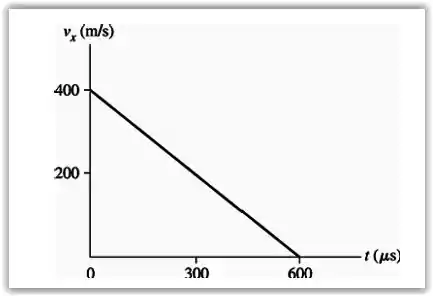
Para entendermos melhor o gráfico:
Quando , a velocidade é igual a velocidade inicial.
Quando , ou seja, o tempo de parada da bala que calculamos no passo anterior, a velocidade é nula.
Faz sentido, né?
Resposta
a)
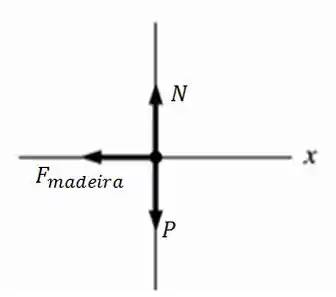
b)
c)