40. Uma caixa de está sobre uma mesa horizontal. Os coeficientes de atrito estático e cinético, entre a caixa e a mesa, são e . A caixa é tracionada por um cabo que faz um ângulo com a horizontal. Determine a força de atrito e a aceleração da caixa se a tensão no fio for: (a) ; (b) .

Podemos obter a tensão no fio sendo uma força que atua a com a horizontal como descrito no enunciado.

Além dessa força temos a força de atrito devido a ação do atrito entre o bloco e a superfície.

E finalmente, como temos a ação da gravidade, temos também a ação da força peso e a ação da força normal.

Desenhando tudo isso em um diagrama de forças, temos

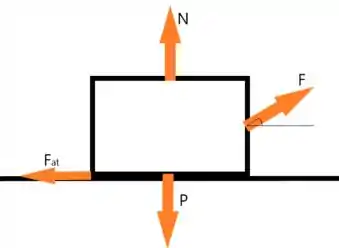
Podemos obter a força de atrito como

Já a força normal pode ser reescrita como

Onde é a componente vertical da força de tração do fio e a força peso ... portanto...

Já para determinar se o bloco está em movimento ou estático, temos que comparar a componente horizontal da força com para , assim, se for maior que , o bloco está se movendo e precisamos mudar o e recalcular e assim, como a força resultante é igual a , se o bloco estiver se movendo temos

A componente horizontal de é dada por

Tranquilo até aqui? 😁

No primeiro caso temos , ou seja

Para , temos que a força de atrito máxima é dada por

Como o bloco está parado e não possui aceleração.

E como o sistema está parado, a força de atrito é igual a .

Bacana, não é? 😐

Agora no segundo caso vamos fazer exatamente a mesma análise, mas agora para .

Calculando a força de atrito para o atrito estático, temos

Comparando com vemos que , portanto o bloco está se movendo dessa vez.

Recalculando a força de atrito para , temos

Assim calculando a aceleração do bloco no segundo caso, vamos obter

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍