PUCRIO, Física 1, P1 – 2019.1, Questão 2, letra a e b; Dinâmica - Leis de Newton
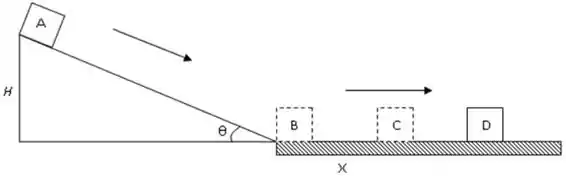
Um bloco de massa M = 35,0 kg encontra-se no topo de um plano inclinado de altura H = 300 cm (sem atrito), o qual faz um ângulo θ = 30° com a horizontal. O bloco está em repouso no ponto A, atingindo o plano horizontal no ponto B com uma velocidade . A partir do ponto B, o bloco desliza sobre uma superfície rugosa com coeficiente cinético μ= 0,4. Após percorrer uma distância X = 5,0 m, o bloco atinge o ponto C com velocidade , passando a interagir com uma mola horizontal de constante elástica k, sendo parado no ponto D após a mola sofrer uma deformação d. ()
- Calcule o módulo da força normal sobre o bloco no trecho . A força normal representa a reação à força peso? Justifique conceitualmente.
- Determine o módulo da aceleração do bloco ao longo do plano inclinado (trecho ). Ela tem o mesmo valor que no trecho ? Justifique.
- Determine o módulo da força de atrito sofrida pelo bloco ao percorrer o plano horizontal no trecho . O valor da força de atrito no trecho é o mesmo que no trecho ? Justifique.
- Determine os módulos de e
Passo 1
- Como nosso bloquinho no trecho AB se encontra num plano incliniado e a força normal é a força de contato com outra superfície, a nossa normal estará oposta ao peso no eixo y! Como o bloquinho ta em equilíbrio no eixo y ( e só temos as forças Peso (em y) e Normal em y em sentidos contrários, temos que . E como sabemos, ! Portanto, temos: E, como já te falei antes, a força normal é a força de Reação a superfície inclinada (nesse caso) do trecho AB, e não ao peso! Fechou? Simbora!
- Como sabemos, se colocarmos um bloquinho num plano inclinado sem atrito, ele provavelmente vai descer pela rampinha, né? Então significa que sua aceleração (que tem o mesmo sentido que a Força Resultante) está na direção da inclinação do trecho AB, ou seja, no nosso eixo X! E quais são as forças que temos no eixo X? Somente o Peso em X, né? Então vamo lá!
- Como o bloco tá em movimento, vamos calcular sua força de atrito cinético! Por definição, sabemos que . No trecho BC, nossa força normal será exatamente o nosso peso, agora não estamos mais num plano inclinado, então temos apenas uma componente do Peso, que está oposta a Normal! Logo = .Então, ficamos com . E como o trecho continua plano e retilínio, a força de atrito permanecerá a mesma, pois ela depende apenas da Normal, e como a Normal não vai mudar, a nossa fat também não!
- Cara, como o corpo saiu do respouso e a gente não tem o tempo podemos usar a equação de torricelli, né? . Massa, mas quem é nosso ?
Passo 2
E fica claro pra gente que a aceleração não vai ser igual nos outros trechos, porque a Força Resultante muda, e consequentemente, a aceleração também! Tranquilo?
Passo 3
Passo 4
Por trigonometria: sen30° = H/ =1/2, então =2H! Como , temos:
Como a=4,9, temos que v=7,7m/s, tranquilo?
E no trecho BC, podemos usar torricelli de novo, só precisamosa achar a aceleração no trecho, que podemos usar nossa força resultante! Show, vamo nessa:
Fechou!
Resposta
- 7,7m/s e 4,5m/s