UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 16b
16. Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo à esquerda. O coeficiente de atrito entre os blocos e o solo é .
b) Determine a aceleração do conjunto e as forças que atuam em cada bloco.
Passo 1
Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema temos dois blocos e com massas e cujo coeficiente de atrito entre os blocos e a superfície é de . Eles são empurrados por uma força horizontal de como foi dado na figura do enunciado.
Com essas informações, queremos determinar a aceleração do sistema de blocos e as forças que atuam em cada bloco.
Tem ideia de como fazer isso? 🤔
Para descobrir a aceleração do conjunto de blocos, temos que aplicar a segunda lei de Newton que nos diz que a força resultante de um sistema é igual a sua massa multiplicada pela sua aceleração, ou seja
Portanto temos que encontrar essa força resultante no sistema.
Bora começar? 😉
Passo 2
A força resultante em um sistema nada mais é que a soma das forças em cada componente.
Como vimos anteriormente, o diagrama de forças dos blocos é dado por
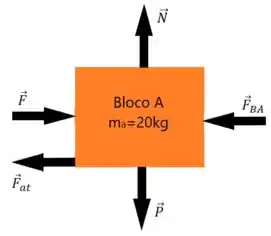
No eixo temos a força que aponta no sentido positivo de , temos também as forças e que apontam em sentidos opostos devido ao contato entre os blocos e por último temos as forças de atrito de cada bloco que que apontam no sentido negativo de e são dadas por
Para o bloco A:
Para o bloco B:
Escrevendo a equação da segunda lei de Newton para encontrar a força resultante em , temos
Como , podemos simplificar a equação como
Se , , e , então
Tranquilo até aqui? 😬
Passo 3
No eixo , no bloco temos a ação da força normal e a força peso, assim como no bloco . Como sabemos que uma força é oposta a outra, podemos afirmar que a força resultante em é igual a .
E finalmente, como a força resultante é igual a massa vezes a aceleração, então
Para o sistema, a massa será a soma de com , ou seja
É isso! Essa resolução te ajudou? Responde Aí! ✌
