Um tijolo repousa sobre uma superfície rugosa e inclinada como mostrado na figura. O módulo da força de atrito que atua no tijolo é:
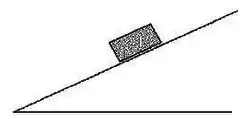
(A) Zero
(B) Igual ao módulo da força peso sobre o tijolo.
(C) Pode ser maior que o módulo da força peso sobre o tijolo.
(D) Deve ser menor que o módulo da força peso sobre o tijolo.
(E) Depende apenas da inclinação do plano inclinado.
Passo 1
Quais são as forças atuando sobre o bloco?
Temos uma força peso para baixo, uma força normal perpendicular à superfície e uma força de atrito :
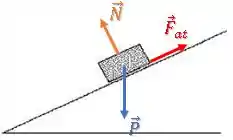
Mas como vamos comparar o módulo dessa força de atrito com o módulo da força peso?
Podemos decompor a força peso nas direções paralela e perpendicular à rampa, assim teremos apenas a força peso e atrito na direção paralela à rampa, o que nos permite compará-las.
Vamos chamar o ângulo de inclinação da rampa de :
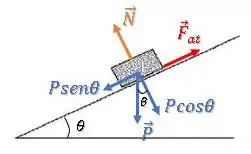
Passo 2
Como o corpo está em equilíbrio, temos que a força resultante sobre ele é nula:
Então, na direção paralela à rampa, temos:
Pronto, conseguimos uma relação entre o módulo da força de atrito e o módulo da força peso.
E qual a conclusão que tiramos disso?
Bom, o módulo da força de atrito é igual à uma componente da força peso.
Como essa componente tem um multiplicado, ela será multiplicado por um número menor do que , então, a força de atrito é menor do que a força peso:
Ficamos com a letra (D).
Resposta
Letra (D)