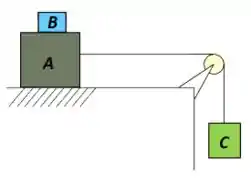
O bloco B, de massa , repousa sob o bloco A, de massa , que por sua vez está sob uma mesa horizontal (figura abaixo). Não existe atrito entre o bloco A e a mesa, porém o coefici- ente de atrito estático entre os blocos A e B é . Uma leve corda é então fixada no bloco A por uma de suas extremidades e passa por uma polia, sem atrito e de massa desprezível, e então suspende o bloco C por sua outra extremidade. Qual a maior massa que o bloco C deve ter para que os blocos A e B continuem deslizando juntos quando o sistema é liberado do repouso?
Passo 1
Eaeeee, belezinha??? Seguinte... a questão nos pede a maior massa que o bloco C deve ter para que os blocos A e B continuem deslizando juntos quando o sistema é liberado do repouso.
Para isso, o sistema deve ter uma aceleração né?
E, para ter a aceleração, tem que haver uma tensão na corda que ultrapasse a força de atrito do bloco B!
Agora vamos lá descobrir!!
Passo 2
Vamos primeiro fazer o diagrama do corpo livre no bloco B:
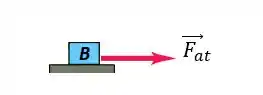
Aplicando a 2ª Lei de Newton no bloco , podemos descobrir a força de atrito :
Passo 3
Agora, podemos descobrir a tensão da corda analisando o diagrama de corpo livre do bloco A:
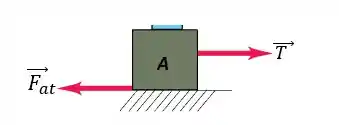
Aplicando a 2ª Lei de Newton no bloco A, podemos descobrir a tensão na corda :
Passo 4
Agora, podemos descobrir a massa do bloco C analisando o diagrama de corpo livre do bloco C:
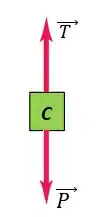
Aplicando a 2ª Lei de Newton no bloco C, temos:
Entendeu direitinho? Responde aee ;)
