UERJ, Sem Campus, Física I, Provas de Física 1 - UERJ - Primeira Prova, Questão 16d
16. Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo à esquerda. O coeficiente de atrito entre os blocos e o solo é .
d) Calcule o trabalho das forças em um arraste de
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos dois blocos e com massas e cujo coeficiente de atrito entre os blocos e a superfície é de . Eles são empurrados por uma força horizontal de como foi dado na figura do enunciado.
Com essas informações, queremos calcular o trabalho realizado por cada força após o sistema se mover por .
Tem ideia de como fazer isso? 🤔
Para calcular o trabalho de uma força, temos
Onde é o ângulo entre a força e o deslocamento.
Vamos analisar cada bloco e as forças que atuam para determinar o trabalho de cada uma.
Bora lá! 😬
Passo 2
Começando pelo bloco , temos
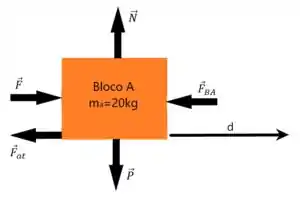
Começando pelas forças que atuam no eixo podemos afirmar que p trabalho delas são iguais a já que essas forças são perpendiculares com o deslocamento , ou seja,
Para
Para
Agora analisando a força , temos que o ângulo entre a força e o deslocamento é , logo
A força de atrito faz um ângulo de com o deslocamento, portanto
Anteriormente calculamos e assim como a força de atrito , ou seja
Tranquilo até aqui? 😉
Passo 3
Agora para o bloco , temos
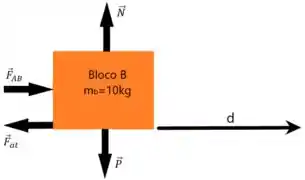
Da mesma forma que vimos anteriormente, as forças que atuam em possuem trabalho igual a
Para a força , temos que o ângulo entre a força e o deslocamento é igual a , portanto . Como , então
Já para a força de atrito , temos que o ângulo entre a força e o deslocamento é igual a , logo
Fim! Iae, o que achou? Responde Aí! 😁
