Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força de Atrito

Ver Teoria
Exercício 50123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495152535455565758

Enunciado

Um plano inclinado que faz um ângulo θ com a horizontal tem uma mola de constante elástica k no seu ponto mais baixo. Um bloco de massa M é liberado próximo ao topo do plano inclinado e se move para baixo comprimindo a mola em ∆ x em relação ao seu tamanho relaxado. O coeficiente de atrito cinético entre o bloco e a superfície do plano inclinado é μ e .

  1. Calcule a energia dissipada pela força de atrito como funções das variáveis dadas no enunciado.
  2. Encontre uma relação entre a compressão da mola ∆ x e a altura H do ponto de onde o bloco é liberado.

Passo 1

Acho que primeiro temos que começar montando um desenho neh? Só assim a gente vei ter uma noção do que fazer mais ampla .

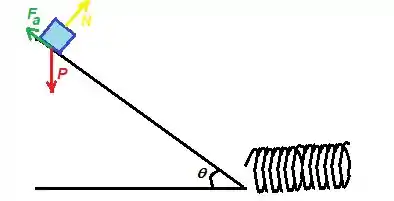
Já aproveitei e inseri aí as forças que estão atuando no bloco nesse momento e P é o peso dele, F a é à força de atrito e N é a força normal do chão ao bloco.

Passo 2

L e t r a   A

POW! Força de atrito pode ser sempre calculada como...

F a = N ⋅ μ e

Nesse caso, só temos que encontrar a força normal! Por trigonometria, repare que...

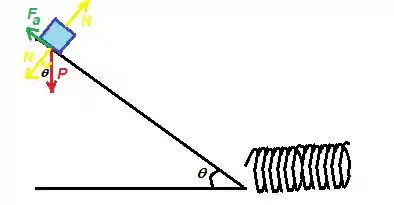
Então, podemos dizer que...

N = P cos ⁡ θ

Então a força de atrito fica...

F a = P cos ⁡ θ ⋅ μ e

Só que e o peso? ORA! Peso é massa vezes a gravidade...

F a = M g μ e cos ⁡ θ

Beleza! Mas como que a gente pode encontrar uma expressão para a energia dissipada pela força de atrito?

Passo 3

Bem, se tivéssemos informação do comprimento d da rampa, podíamos usar a expressão do trabalho, pois a energia dissipada seria...

E d = F a d

Mas sabemos que a rampa tem altura H , pois foi dado no item b ...

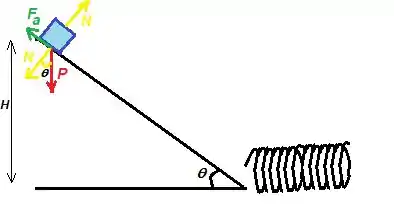
Por trigonometria com o triângulo grande...

H d = sin ⁡ θ   →

d = H sin ⁡ θ

Então a energia dissipada na rampa em função dos dados será...

E d = F a H sin ⁡ θ   →

E d = M g μ e cos ⁡ θ H sin ⁡ θ   →

E d = M g H μ e cot ⁡ θ

Passo 4

Cara, pensa no seguinte. No início. Quando a mola foi posta no topo, ela só tinha energia potencial E p . Ela começou a deslizar e transformou essa energia potencial em cinética E k e energia térmica (energia dissipada pela força de atrito)...

E p = k + E d

Mas então, ao chegar na mora, a energia que cinética, foi transformada em energia potencial Elástica...

E p = E e l + E d

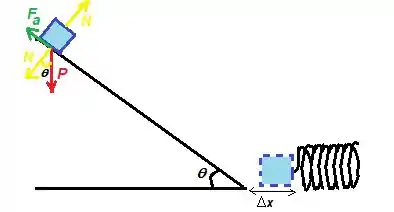
A energia potencial elástica, de acordo com a teoria é...

E e l = 1 2 k ∆ x 2

E a energia potencial gravitacional é E p = M g H ...

M g H = 1 2 k ∆ x 2 + M g H μ e cot ⁡ θ

Dividindo todo mundo por M g então...

H = 1 2 M g k ∆ x 2 + H μ e cot ⁡ θ

Passando essa expressão pro outro lado...

H - H μ e cot ⁡ θ = 1 2 M g k ∆ x 2     →

H 1 - μ e cot ⁡ θ = 1 2 M g k ∆ x 2     →

Então...

H = k 2 M g 1 - μ e cot ⁡ θ ∆ x 2

Prontinho! Essa é a relação de H com ∆ x . Podemos isolar em termos do ∆ x ...

2 M g 1 - μ e cot ⁡ θ k   H = ∆ x 2     →

∆ x = 2 M g 1 - μ e cot ⁡ θ k   H

Varia com a raiz de H

Resposta

Letra A:

E d = M g H μ e cot ⁡ θ

Letra B:

∆ x = 2 M g 1 - μ e cot ⁡ θ k   H

Exercícios de Livros Relacionados

12.17P A mesma esfera descrita no Problema 12.16 submerge em óleo SAE 30 à temperatura de 20 °C , cuja densidade é aproximadamente igual á da água. A) Calcule a velocidade terminal da esfera. B) Calcu
12.9E Uma pare-quedista com massa de 60kg salta com um paraquedas cuja área frontal é de 15m² ². Sabendo que a densidade do ar é ρ = 1,2kg.m³ ³ e que o coeficiente de arraste do paraquedas é C = 1,4 ,
Um operário arrasta um caixote no piso de uma fábrica puxando-o por uma corda. O operário exerce uma força de módulo F = 450N sobre a corda, que está inclinada de um ângulo θ = 38 ° em relação à horiz
Um caminhão transporta um caixote de 200k g a 90k m / h numa estrada horizontal. Avistando um obstáculo, o motorista fria, com desaceleração uniforme de 2,5m / s 2 , até parar. O caixote, em consequên
12.7E Uma placa de vidro molhada com área de 2,0m² ² é colocada sobre outra placa idêntica, e um filme de água com espessura de 3,0μm se forma entre elas. Uma força de cisalhamento de 50N é aplicada à