A força que atua sobre uma partícula depende da posição da partícula no plano . Essa força é dada por
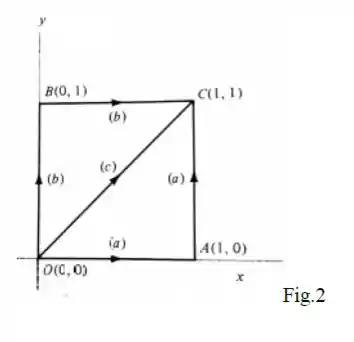
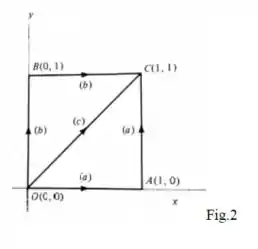
onde x e y são expressos em metros. Calcule o trabalho realizado por esta força quando a partícula se move, conforme Figura 2, do ponto O ao ponto C ao longo
(a) do caminho ;
(b) do caminho e
(c) do caminho
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá essa força aqui
E pede o trabalho da partícula no caminho
 E agora?
E agora?
Vamos lembrar que o trabalho é um produto escalar entre a força e o vetor deslocamento:
Então precisamos determinar um vetor que descreva o deslocamento pedido e fazer o produto escalar com a força!

Beleza?
Bora lá!
Passo 2
Olhando pro caminho temos associados dois vetores deslocamentos!
Fazendo o produto temos
E é isso! Até a próxima!