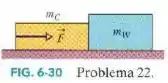
Na Fig. 6-30, uma caixa de cereal Cheerios (massa ) e uma caixa de cereal Wheaties(massa ) são aceleradas sobre uma superfície horizontal por uma força aplicada a caixa de cereal Cheerios. O módulo da força de atrito que age sobre a caixa de Cheerios é de , e o módulo da força de atrito que age sobre a caixa de Wheaties é de . Se o módulo de é de , qual é o módulo da força que a caixa de Cheerios exerce sobre a caixa de Wheaties?
Passo 1
O normal a se fazer em questões com corpos em contato dessa maneira é partir pro braço e desenhar os diagramas de corpo livre. Essa não é diferente, mas temos que reparar uma coisa antes, porque se não chegaremos ao fim e faltará uma informação.
Os blocos andam juntos e, portanto, realizam o mesmo deslocamento. Isso garante que ambos os blocos possuem a mesma aceleração.
Com essa informação vamos ao diagrama de corpo livre de cada bloquinho, guardando as equações para montar um sisteminha no final e encontrar o módulo da força que a caixa de Cheerios exerce sobre a caixa de Wheaties.
Passo 2
Reparado o detalhe acima, podemos desenhar o diagrama de corpo livre de cada bloco.
Começaremos com o do cereal Cheerios, temos a força empurrando o bloco pra frente e a força que a caixa de Wheaties faz na caixa de Cheerios que chamaremos de empurra a caixa pra trás.
Também representaremos a força de atrito cinético como oposta ao deslocamento.
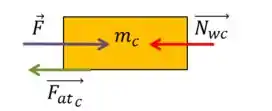
E aplicando a segunda lei de Newton, chegamos a:
E, considerando que para direita será positivo e que a aceleração é igual a aceleração do sistema , teremos:
Substituindo os valores de , e de , temos:
Passo 3
Já na caixa de Wheaties, temos o seguinte diagrama:
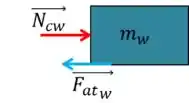
Aqui temos a força que a caixa de Cheerios faz na caixa de Wheaties , que é a força que o enunciado pede, ela está empurrando a caixa pra frente, também temos a força de atrito cinético se opondo ao movimento da caixa.
E aplicando novamente a segunda lei de Newton:
E considerando novamente para direita positivo e que será a aceleração do sistema .
Substituindo os valores de e de :
Passo 4
Pela terceira lei de Newton, sabemos que as forças de ação e reação são iguais em módulo:
Juntando as equações, temos:
Enfim encontramos o módulo da força que queríamos: