UFSCAR, Sorocaba, Física 1, Listas de Física 1 - UFSCAR (Sorocaba) - Lista 3, Questão 6
Um bloco de massa é puxado com velocidade constante sobre uma superfície horizontal por um cordão, conforme figura 6. Determine a magnitude da força de atrito.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um bloco de massa que é puxado por um cordão com velocidade constante, ou seja, com aceleração ZERO!!
A questão nos pede para determinarmos a magnitude da força de atrito. E aí? Tem alguma ideia de como podemos resolver?
Bom... uma forma é analisar as forças que atuam sobre o bloco e utilizar a Segunda Lei de Newton:
Onde é a força, é a massa e é a aceleração.
Não entendeu? Então bora junto 😉
Passo 2
Bom... fazendo o diagrama de corpo livre, temos:
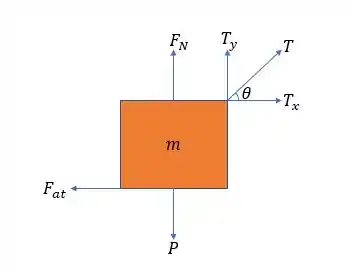
Onde:
- é a força normal;
- é o peso;
- é a força de atrito;
- é a tração da corda;
- e são as componentes de .
Passo 3
Do diagrama de corpo livre, aplicando a Segunda Lei de Newton, temos:
Como a aceleração é , então:
Passo 4
Da segunda equação, temos:
Sabendo que a força de atrito é dada por:
Onde é o coeficiente de atrito.
Substituindo em , temos:
Entendeu direitinho? Responde aee ;)
