[ENUNCIADO COMUM ÀS QUESTÕES 5 e 6]
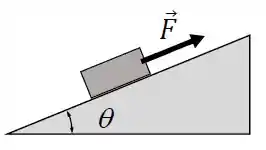
Um bloco de massa está em movimento ao longo da superfície de um plano inclinado que faz um ângulo com a horizontal e está submetido a uma força .
[QUESTÃO 5]
Sabendo que a força de atrito tem módulo e sentido de baixo para cima do plano inclinado, é a aceleração da gravidade e , então o módulo da aceleração do bloco é
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Queremos a aceleração do bloco. Então, vamos analisar as forças atuando sobre ele.
Temos a força peso para baixo, a força normal perpendicular à superfície da rampa e a força de atrito para cima da rampa (enunciado):
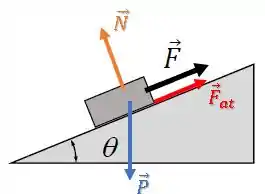
Passo 2
A aceleração do bloco está na direção da rampa, então vamos decompor a força peso para que a gente possa usar apenas componentes no eixo paralelo à rampa (direção da ) e perpendicular a ela.
Podemos decompor o vetor usando o ângulo de inclinação da rampa :
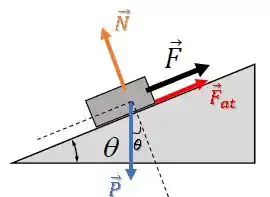
Ficamos com as componentes:
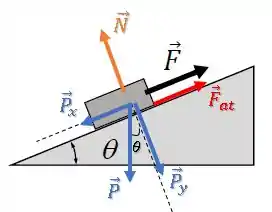
Passo 3
Mas para qual sentido o bloco está deslizando?
Bom, se a força de atrito está para cima da rampa, isso significa que ela está atuando contra o deslizamento do bloco (para baixo).
Então, a aceleração do bloco está no sentido de descida da rampa.
Vamos aplicar a Segunda Lei de Newton na direção paralela à rampa:
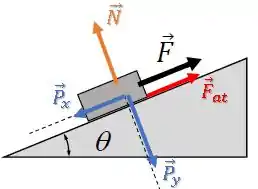
A componente é:
A força peso é dada por :
Por fim, achamos que a aceleração é:
Ficamos com a alternativa (a).
Resposta
Letra (a)