Na figura abaixo, a força aplicada sobre a caixa tem módulo constante igual a . A massa da caixa é . Existe atrito entre o solo e a caixa. O coeficiente de atrito cinético é igual a 0,47.
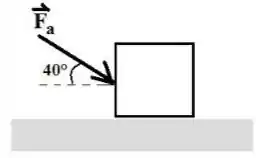
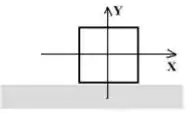
a) Represente o diagrama de corpo livre da caixa (colocando as forças que agem sobre a caixa na origem do sistema de coordenadas indicado).
b) Calcule o vetor força (usando vetores unitários) que o solo faz sobre a caixa.
c) Calcule o vetor aceleração da caixa.
Passo 1
a)
As forças que atuam no bloco além da força são a força normal, peso e força de atrito.
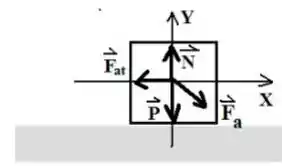
Passo 2
b)
A força que o solo faz sobre a caixa é a soma da força Normal e da força de atrito.
A primeira coisa que temos que verificar é se a caixa está em movimento, pra sabermos se essa força de atrito em questão é de fato a cinética. Vamos supor que a caixa esteja sim em movimento na horizontal. Nesse caso:
Mas:
Ou seja, a caixa não está em movimento.
Sendo assim, a força de atrito tem módulo igual à .
Para o cálculo do módulo da força normal observamos que no eixo a soma das forças também deve ser nula:
Passo 3
c)
Para calcular o vetor aceleração, precisamos saber o valor da resultante que age sobre a caixa.
Como sabemos que a resultante é nula, a aceleração é nula.
Resposta
a) 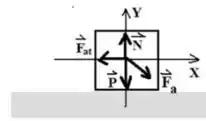
b)
c)