UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 16.
16 – Um ioiô de massa tem um carretel de raio e um eixo de raio . O seu momento de inércia passando pelo centro do ioiô e paralelo ao seu eixo pode ser aproximado por . O ioiô é colocado num plano inclinado de ângulo com respeito a horizontal e seu fio é puxado com uma força de magnitude e paralela ao plano inclinado de forma que o ioiô role. A aceleração da gravidade tem magnitude . O coeficiente de atrito estático entre o ioiô e o plano inclinado é .
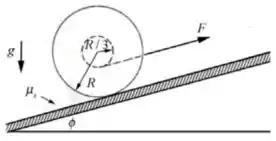
Qual é a máxima magnitude da força que o ioiô é puxado sem que ele deslize? Expresse sua resposta em termos dos dados do exercício.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão, temos um ioiô sob um plano inclinado que possui atrito. No eixo do ioiô uma corda é enrolada e puxada na direção subindo o plano. Com as informações dadas no enunciado, temos que obter qual deve ser a maior torça de modo que o torque resultante não faça o ioiô deslizar.
E aí, tem alguma ideia do que podemos fazer? 🤔
Para calcular o torque de um ioiô sendo puxado na direção contrária ao movimento sob um plano inclinado com atrito, precisamos levar em consideração algumas variáveis e fórmulas importantes.
Primeiro, precisamos entender que o torque é definido como a força aplicada em um objeto multiplicada pela distância entre o ponto onde a força é aplicada e o eixo de rotação.
Lembra disso? 👀
Passo 2
No caso do ioiô, podemos considerar o ponto em que a força é aplicada como sendo a corda que está sendo puxada, enquanto o eixo de rotação seria o ponto onde a corda está presa ao ioiô.
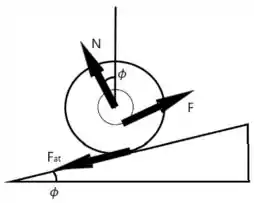
Para determinar a força que está sendo aplicada na corda, precisamos considerar a força de atrito que está agindo sobre o ioiô. Essa força de atrito é igual ao produto entre o coeficiente de atrito entre o ioiô e o plano inclinado e a força normal exercida pelo plano inclinado sobre o ioiô.
A força normal pode ser calculada pela decomposição do peso do ioiô ao longo do plano inclinado. A componente do peso perpendicular ao plano inclinado é igual à força normal, enquanto a componente paralela ao plano inclinado é igual à força de atrito.
Assumindo que o ioiô esteja em movimento uniforme, podemos concluir que a força de tração exercida pela mão do usuário é igual à força de atrito. Portanto, podemos igualar as duas equações e resolver para o torque:
Substituindo em
Assim, para que não haja deslizamento, o torque gerado pela rotação do ioiô no plano deve ser maior que o torque gerado pela força .
Isolando e simplificando ...
É isso! Essa resolução te ajudou? Responde Aí! ✌
