USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 42d
42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .
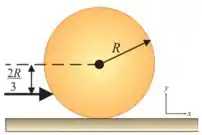
(d) Qual o trabalho da força de atrito?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos uma bola de massa e raio parada em uma mesa. Ela recebe um impacto horizontal a uma distância abaixo do seu centro com a bola adquirindo uma velocidade e uma rotação.
Com isso queremos descobrir qual é o trabalho realizado pela força de atrito.
Lembra como fazemos isso? 👀
Pela ideia de conservação de energia, a energia inicial do sistema é igual a energia final menos as perdas que ocorreram no caminho, ou seja
Assim podemos dizer que as perdas são
Justamente a energia de perdas do nosso sistema é o trabalho realizado pela força de atrito então sabendo a energia inicial e a energia final, podemos obter o trabalho de ...
Bora começar! 😁
Passo 2
Anteriormente calculamos que a energia inicial do sistema era
Então temos que nos preocupar apenas em calcular a energia final do sistema...
No instante quando a bola para de deslizar, a energia que o sistema compõe é dada pela energia cinética de rotação e a energia cinética de translação, ou seja
A energia cinética de translação é obtida a partir da equação
Já a energia cinética de rotação, pela equação
Substituindo em
Sabemos que o momento de inercia de uma esfera é dada por
E também calculamos anteriormente que a velocidade linear final é dada por
Logo, pela relação entre a velocidade linear e a velocidade angular, podemos encontrar como
Tranquilo até aqui? 😬
Passo 3
Substituindo essas informações em
Simplificando...
Como foi dito que e
Assim, como
Fim! Iae, o que achou? Responde Aí! 😁
