UFSCAR, Sorocaba, Física 1, Listas de Física 1 - UFSCAR (Sorocaba) - Lista 3, Questão 9b
Considere e o coeficiente de atrito estático entre o bloco e o plano é .
(b) Encontre a força de atrito sobre o bloco de se .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um sistema de dois blocos de acordo com a seguinte figura:
Desejamos descobrir a força de atrito sobre o bloco de se .
Para isso, precisamos analisar o diagrama de corpo livre de cada bloco e aplicar a Segunda Lei de Newton para o sistema em equilíbrio (aceleração zero!!).
Não entendeu? Então bora junto 😉
Passo 2
Bom... fazendo o diagrama de corpo livre para os dois casos, temos:
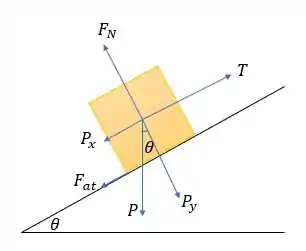
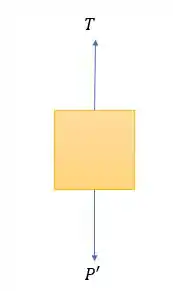
Onde:
- é a força normal;
- é o peso;
- é a força de atrito;
- é a tração da corda;
- e são as componentes de .
Passo 3
Pelo diagrama de corpo livre do bloco da segunda imagem e a Segunda Lei de Newton, temos:
Por outro lado, pelo diagrama de corpo livre do bloco da primeira imagem, temos:
Obs: O sinal negativo indica apenas que a força é oposta ao sentido adotado.
Entendeu direitinho? Responde aee ;)
