- Seja uma função infinitamente derivável. Suponha que a série de Taylor da centrada em seja dada pela série
- Qual o intervalo de convergência desta série? (Não se esqueça de avaliar os extremos do intervalo).
Passo 1
Fala aí, galerinhaa!
Esse problema é sobre convergência dessa série aqui
Bom... o problema nos fala que a série é centrada em e a gente sabe que o raio de convergência dessa série é:
Esse raio de convergência dos diz os possíveis valores de ao redor de onde a série está centrada em que a série é convergente. A gente tem uma estrutura tipo essa aqui:
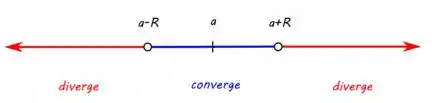
O que a gente não pode esquecer é que naqueles pontos em branco e (os extremos do intervalo) a gente tem que dar uma atenção maior, ok?
Então partiu resolver essa!!
Passo 2
Bom, primeiro vamos ver onde estão os extremos do nosso intervalo de convergência:
Usando e temos o intervalo de convergência sendo:
E os extremos são e , resta agora saber se quando vale algum desses valores a série é convergente ou não. Isso vai dizer se eles estão ou não no intervalo, ok?
Passo 3
Vamos começar com usando esse valor na série temos:
Arrumando um pouco temos:
Como vai ser sempre um número ímpar, sabemos que:
Então a série fica com essa cara aqui:
A série que apareceu é uma p-série com e a gente sabe que uma série desse tipo é divergente, ou seja, faz com que a série seja divergente, então ele não entra no intervalo de convergência!
Passo 4
Para a série de potências se torna:
Se avaliarmos alguns termos dessa série a gente observa um padrão:

JÁ SEEEI! uma séria harmônica alternada né? A gente sabe que ela é convergente!Então nos dá uma série convergente então ele entra no intervalo de convergência. Com o que a gente já calculou temos o intervalo de convergência sendo:
E aí resolvemos essa 😊 Vamos para a próxima??