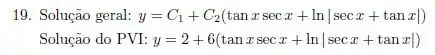Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método de Redução de Ordem

Ver Teoria
Exercício 2512345678910111213141516171819202122232426272829303132333435

Enunciado

Passo 1

O método de redução de ordem nos diz que a nossa solução será na forma

y 2 x = ϕ x y 1 ( x )

y 2 x = ϕ

Vamos calcular y ' ' para substituir na nossa equação.

y 2 ' = ϕ '

y 2 ' ' = ϕ ' '

Passo 2

Substituindo a derivada na nossa EDO.

y ' ' - 3   tan ⁡ x y ' = 0

ϕ ' ' - 3 ϕ ' tan ⁡ x = 0

Para colocar essa equação no formato de EDO de primeira ordem, vamos fazer uma substituição.

u = ϕ '

u ' = ϕ ' '

u ' - 3 u   ( tan ⁡ x ) = 0

Passo 3

Agora só precisamos resolver a EDO linear de primeira ordem normalmente. Neste caso temos uma EDO separável.

u ' - 3 u   ( tan ⁡ x ) = 0

d u d x = 3 u tan ⁡ x  

d u u = 3 tan ⁡ x d x

Integrando de ambos os lados

ln ⁡ u = 3 ln ⁡ sec ⁡ x + C

ln ⁡ u = ln ⁡ sec ⁡ x 3 + C

u = C s e c 3 x

Passo 4

Precisamos então encontrar ϕ a partir de u .

ϕ ' = u

ϕ ' = C sec 3 ⁡ x

Integrando os dois lados teremos

ϕ = C 2 ln ⁡ tan ⁡ x sec ⁡ x + sec ⁡ x tan ⁡ x + C '

ϕ = C 1 ln ⁡ tan ⁡ x sec ⁡ x + sec ⁡ x tan ⁡ x + C 2

Como

y 2 = ϕ

y 2 = C 1 ln ⁡ tan ⁡ x sec ⁡ x + sec ⁡ x tan ⁡ x + C 2  

Essa é nossa solução geral.

Passo 5

Agora podemos resolver o PVI utilizando as condições iniciais.

y 0 = 2

y ' 0 = 6

y ( 0 ) = C 1 ln ⁡ tan ⁡ 0 sec ⁡ 0 + sec ⁡ 0 tan ⁡ 0 + C 2  

C 2 = 2

y ' 0 = C 1 sec 3 ⁡ 0 = 6

C 1 = 6

Então nossa solução é

y = 6 ln ⁡ tan ⁡ x sec ⁡ x + sec ⁡ x tan ⁡ x + 2

Resposta

Exercícios de Livros Relacionados

Encontre a solução geral da equação diferencial dada. y ' ' - 2 y ' + 10 y = 0
Se ar² + br + c = 0 tem raízes iguais r1, mostre queComo a última expressão à direita na Eq. (i) é nula quando r = r1, segue que exp(r1t) é uma solução de L[y] = ay′′ + by′ + cy = 0.
Use o método de redução de ordem para encontrar uma segunda solução da equação diferencial dada.
Use a fórmula de Abel [Eq. (23) da Seção 3.2] para mostrar que o wronskiano de duas soluções quaisquer da equação dada é em que c1 é constante.
Considere o problema de valor inicialEncontre as coordenadas do ponto de máximo (tM, yM) em função de b. Descreva a dependência em b de tM e de yM quando b aumenta.