60. Como fica a relação abaixo para n eventos quaisquer
Passo 1
Primeira coisa: Não pira!
O enunciado pede a relação para eventos quaisquer, mas vamos olhar primeiro essa relação? Tá, vamos lá...
Essa relação é verdadeira? Bom, pelo enunciado parece que sim, mas vamos entender ela.
Vamos olhar para o lado direito primeiro e ver como podemos “abrir” essa equação. Podemos começar aplicando a fórmula de probabilidade condicional com :
Também podemos abrir o , com a mesma fórmula de probabilidade condicional:
Então, vamos substituir esses valores na equação que temos e ver o que encontramos:
Corta bastante coisa né?
Cancelando cada lado teremos que:
Ok, sabemos que essa relação é coerente!
Passo 2
Agora que entendemos melhor o mecanismo, vamos olhar para o caso com quatro eventos... A ideia de olhar para quatro é ver o que muda e como muda para conseguir fazer uma analogia com o caso com n eventos ok? Vamos fazer o caminho inverso agora:
Bom, podemos isolar o lado esquerdo:
Agora vamos aplicar a fórmula da probabilidade condicional:
Então
Substituindo :
Reorganizando
Notamos então que ao fazermos para quatro eventos, acrescentamos uma parcela. E essa parcela é algo do tipo:
Percebe-se que se fizermos para cinco eventos iremos acrescentar um termo análogo a esse na expressão e assim por diante. Veja só o esquema abaixo:
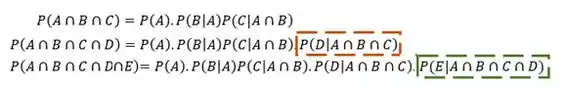
Notamos que esse é o termo que é acrescentado a nossa expressão. Assim podemos pensar no caso geral né?
Passo 3
Pro caso geral então teremos:
Resposta
Ei, a resposta está no passo a passo :)