O receptor de um determinado equipamento de uma rede de telecomunicações recebe mensagens de instruções através de três possíveis transmissores diferentes. Estatísticas da rede mostram que 50% das mensagens recebidas são enviadas pelo transmissor 1, 40% pelo transmissor 2 e 10% pelo transmissor 3. Para fins de garantia de integridade das informações, o protocolo de comunicação exige que o receptor confirme o recebimento repetindo ao seu transmissor a mensagem recebida.
Entretanto, a chance de os transmissores enviarem mensagens contendo erros nos bits que os identificam é de 1%, 3% e 6%, respectivamente. Com base nessas estatísticas, pede-se:
a) Fazer o diagrama de Venn.
b) Qual é a probabilidade de chegar uma mensagem no receptor com erro na identificação do remetente e, portanto, o receptor não ter certeza sobre qual transmissor ele deve responder?
c) Para cada um dos três transmissores, qual a probabilidade de este ter sido o remetente de uma mensagem que chegou no receptor com erro na identificação?
Passo 1
Fala galerinha, beleza? Bora resolver uma questão de prova!
Nesse problema vamos brincar um pouco com o diagrama de Venn. Temos que considerar as duas situações descritas no problema: a região dentro do retângulo corresponde a mensagem com erro na identificação (as fora são mensagens sem erro), enquanto os círculos representam os transmissores:
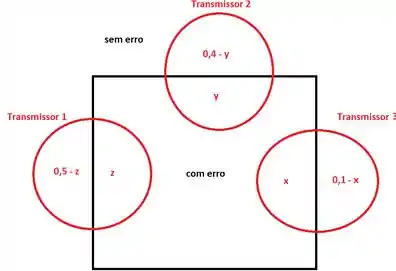
Como a probabilidade de a mensagem ser do transmissor 1 é , se é a probabilidade de a mensagem conter erro e ser do transmissor 1, temos que é a probabilidade de a mensagem não conter erro e ser do transmissor 1. Seguindo a mesma lógica, construímos o resto do diagrama.
Passo 2
A probabilidade do transmissor 1 enviar uma mensagem com erro é . Com isso, temos que
Deixa eu dar uma explicadinha um pouco melhor sobre essa última conta: quando consideramos o transmissor 1, nosso espaço amostral se reduz a . Dentro desse espaço amostral, o erro é representado pela letra . Daí a probabilidade .
Fazendo os mesmo para os demais transmissores:
Com isso, podemos escrever o diagrama completo:
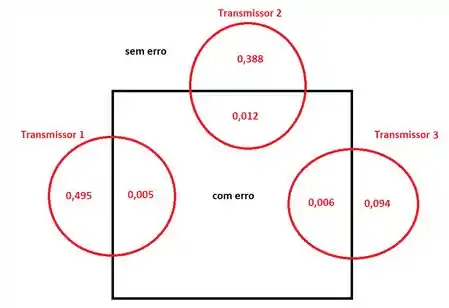
Passo 3
Vamos responder o item (b): a probabilidade de chegar uma mensagem com erro é a soma das probabilidades de erro em cada transmissor:
Assim,
No item (c), temos que calcular a probabilidade de a mensagem ter vindo de cada transmissor dado que ela veio com erro. Para isso, usamos a fórmula da probabilidade condicional:
Nesse caso, o espaço amostral é . Os numeradores das probabilidades serão , e . Logo, temos que
Isso finaliza o problema 😉!