Uma empresa de desenvolvimento urbano considera a possibilidade de construir um shopping center num setor do Rio de Janeiro. Um elemento vital é uma proposta em um setor com estrada que liga ao centro da cidade.
Se o Conselho aprovar essa rodovia, há probabilidade da empresa construir o shopping, enquanto, se a rodovia não for aprovada a probabilidade é de apenas .
Com base em informações disponíveis, o presidente da empresa estima que uma chance que a estrada seja aprovada.
Pede-se:
a) Fazer o Diagrama de Venn (partição evento – evento bolota).
b) Qual é a probabilidade de a empresa construir o shopping?
c) Uma vez que o shopping foi construído, qual é a probabilidade de que a rodovia seja aprovada?
Passo 1
Fala galerinha, beleza? Bora resolver uma questão de prova!
Nesse problema vamos brincar um pouco com o diagrama de Venn. Temos que considerar dois eventos no problema: a aprovação da rodovia e a construção do shopping. Com isso, o diagrama de Venn será algo do tipo
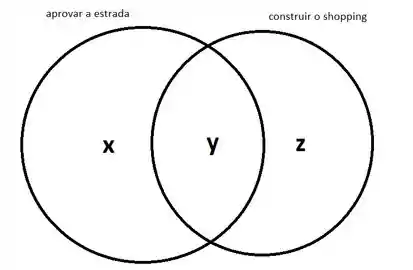
Nessa representação, é a probabilidade de apenas a estrada ser aprovada (sem a construção do shopping), é a probabilidade de shopping ser construído sem a aprovação da estrada e é a probabilidade de ambas as coisas acontecerem.
No texto, foi dito que a probabilidade de a estrada ser aprovada é , de modo que
A probabilidade de a empresa construir o shopping dado que o Conselho aprovou a rodovia é
Para entender essa última relação, é legal você ter uma ideia de probabilidade condicional. Quando ele fala que o Conselho aprovou a rodovia, nosso espaço amostral se reduz a . Dentro desse espaço amostral, o shopping é construído apenas na situação descrita por . Daí a fração que escrevemos acima!
Já se o conselho não aprovar a rodovia, o espaço amostral se reduz a
Com isso, a probabilidade de o shopping ser construído dado que a rodovia não foi aprovada é
Agora temos todas as equações que precisamos para resolver o problema!
Passo 2
Como , temos que
Da mesma forma,
Com isso, podemos completar o diagrama de Venn:
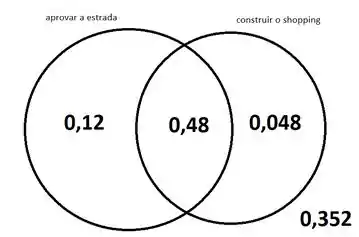
Observe que a probabilidade de nem a estrada ser aprovada e nem o shopping ser construído é
Passo 3
O item (a) já foi resolvido, bora pros demais itens! A probabilidade de a empresa construir o shopping é
Portanto,
Para terminar, no item (c) ele pergunta qual a probabilidade de a estrada ser aprovada dado que o shopping foi construído. Trata-se de uma probabilidade condicional:
Logo,
Portanto,
Com isso a gente finaliza o problema 😉!