Prova P1 – 2019.1– USP – Probabilidades – Teste 5
Eu tenho duas moedas: uma delas é honesta, e a outra tem cara nas duas faces. Eu escolho uma das duas moedas ao azar, arremesso-a duas vezes, e nas duas vezes aparece cara. A probabilidade de que eu tenha escolhida a moeda honesta é:
Passo 1
Faaalaeee menó, beleza?
Vamos deixar de início uma coisa bem clara, belezinha? Se liga... temos duas moedas:
- Moeda 1: Cara ou coroa ;
- Moeda 2: apenas cara .
Como sabemos que saíram duas caras, desejamos saber a probabilidade condicional a seguir:
Ou seja, queremos a probabilidade de a moeda ser honesta, dado que saíram duas caras.
Passo 2
Dessa forma, temos:
Sendo que:
E que:
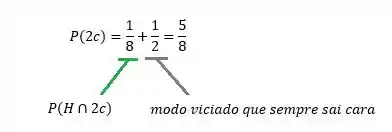
Logo, substituindo na primeira equação, temos:
Entendeu direitinho??? Valeeeu!
Resposta
Exercícios de Livros Relacionados
Verifique pelas Eqs. (3.2) que, sendo A fixo, P ( B | A ) satisfaz aos vários postulados da probabilidade.
Um artigo na British Medical Journal “Comparison of treatment of renal calculi by operative surgery, percutaneous nephrolithotomy, and extracorporeal shock wave lithotripsy” - Comparação de tratamento
A urna 1 contém x bolas brancas e y bolas vermelhas. A urna 2 contém z bolas brancas e v bolas vermelhas. Uma bola é escolhida ao acaso da urna 1 , e posta na urna 2 . A seguir, uma bola é escolhida a
Demonstre: Se P (A| B )P (A) , então P (B| A )P (B) .
Um mecanismo pode ser posto em uma dentre quatro posições: a ,b ,c e d . Existem 8 desses mecanismos incluídos em um sistema. ( a ) De quantas maneiras esse sistema pode ser disposto? ( b ) Admita que