15) Deseja-se projetar um filtro de spam para uma conta de e-mail. Para isso, realizou-se um estudo probabilístico baseado na presença de determinadas palavras-chave (por exemplo, Viagra, você ganhou, etc.) nas mensagens recebidas. A partir desse estudo, conclui-se que a probabilidade das mensagens de spam conterem alguma dessas palavras-chave é . Curiosamente, a probabilidade das mensagens que contém essas palavras serem spam também vale .Constatou-se ainda que a probabilidade de mensagens que não são spam conterem essas palavras é A probabilidade de uma mensagem dessa conta de e-mail ser spam é de:
a)
b)
c)
d)
e)
Passo 1
Eaí gente, tudo certinho com vocês?
Nessa questão a gente tem uma situação bem interessante sobre as mensagens spam que chegam no e-mail. A ideia é tentar filtrar os spams com base em palavras-chave muito comuns em mensagens desse tipo.
Mas, pra nossa área aqui da probabilidade, são dadas várias informações e fica até um pouco confuso tentar separar todas elas mentalmente.

Uma dica nesse tipo de situação é montar um esquema, tipo uma árvore de probabilidade mesmo, pra conseguir visualizar melhor o que está acontecendo. Então, vamos fazer isso!
Passo 2
Bora começar identificando as informações.
) A probabilidade das mensagens de spam terem alguma palavra-chave é de .
) A probabilidade de uma mensagem que não é spam ter alguma palavra-chave é de .
Beleza, com isso já podemos montar o primeiro esquema, tendo cuidado pra sempre que possível calcular a probabilidade do ramo complementar.

Onde é justamente o que queremos descobrir: a probabilidade de uma mensagem ser spam.
Muito bom! E ainda tem uma informação que podemos analisar:
) A probabilidade de mensagens que contém alguma palavra-chave também ser spam é de .
Aqui tem que ter cuidado. O que ele tá falando é que dado um e-mail que possui palavra-chave, então a probabilidade dele ser spam é de .
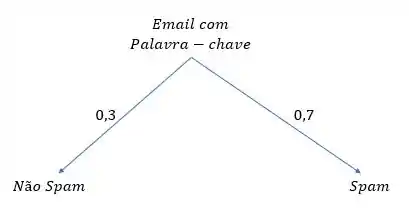
Ótimo! Agora que esquematizamos as informações em árvores de probabilidade está mais tranquilo para interpretá-las.
Passo 3
Aqui o nosso objetivo é conseguir, a partir das árvores, escrever uma equação que nos ajude a determinar .
A probabilidade da informação é:
Mas, segundo a primeira árvore que desenhamos, temos que:
Top demais! Substituindo isso em , ficamos com:
Aeeee, conseguimos determinar a probabilidade de uma mensagem que chega nesse e-mail ser spam. Muito bom, galera! Até a próxima, tamo junto!
Resposta
Letra C: