Uma certa forma de câncer ocorre à razão de 3 em 1000 pessoas. Desenvolveu-se um teste para
detectar a doença, se um paciente é sadio existe 4% de chance de um alarme falso, e se um paciente tem a doença existe 3% de chance de que o teste não consiga detectá-la.
Pede-se
a) Fazer o diagrama de Venn.
b) Qual a probabilidade de a pessoa ter a doença sabendo que o resultado do teste foi positivo (acusou a existência da doença)?
Atenção – o resultado deste problema vai ser surpreendente.
Passo 1
Fala galerinha, beleza? Bora resolver uma questão de prova!
O primeiro passo é saber que a probabilidade de uma pessoa ter a doença é , enquanto a probabilidade dela ser saudável é . Vamos chamar de a probabilidade de a pessoa ser doente, porém o teste dar errado (indicando que ela é saudável). Nesse caso, a probabilidade de uma pessoa ser doente e o teste indicar o resultado correto é .
Da mesma forma, se for a probabilidade de a pessoa ser saudável e o teste dar errado (indicando que ela é doente), temos que é a probabilidade de pessoa ser saudável e o teste indicar um resultado correto (que ela não é doente). Com isso, construímos o diagrama de Venn:
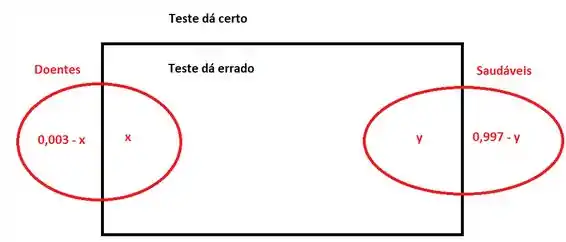
Dentro do retângulo temos os testes errados e fora os testes certos. Os círculos representam as pessoas doentes e saudáveis. Repare que
O que faz total sentido, certo? A soma de todas as probabilidades deve ser um!
Passo 2
Se um paciente é sadio, existe de chance de um alarme falso. Como o paciente é sadio, o espaço amostral se reduz a . A probabilidade de um teste dar errado dado que uma pessoa é saudável é
Como e , temos que
Por outro lado, caso o paciente tenha a doença, a probabilidade de o teste dar errado é . Assim,
Estou considerando 4 casas decimais, por isso o arredondamento. O diagrama de Venn completo fica:
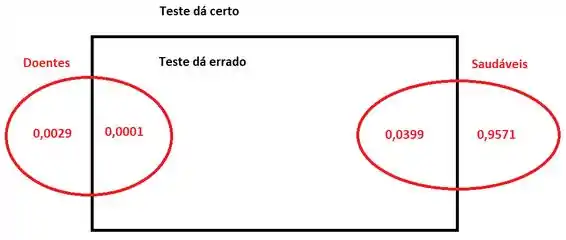
Passo 3
No item (b), ele quer saber qual é a probabilidade de a pessoa ter a doença dado que o teste deu positivo. Primeiro calculamos a probabilidade de o teste dar positivo. Isso pode ocorrer de duas formas: a pessoa é doente e o teste dá certo ou a pessoa é saudável e o teste dá errado:
Assim,
A probabilidade de a pessoa ter a doença dado que o teste deu positivo é
Logo,
Repare que o resultado é bem curioso: se você faz o teste e dá positivo, a chance de você estar doente ainda é bem baixa: . Isso está de acordo com a nota de rodapé do enunciado 😉.