02) Dois números, e , são gerados aleatoriamente e uniformemente distribuídos no intervalo . Assuma que são gerados de maneira independente e calcule a probabilidade da equação possuir raízes reais.
a)
b)
c) .
d)
e)
Passo 1
Faaala pessoal, como vocês estão?
Essa questão é bem complicadinha, mas vem comigo que vamos deixar ela tranquila tranquila haha!

Basicamente, temos duas variáveis aleatórias e , que seguem uma distribuição uniforme no intervalo e que são coeficientes da seguinte equação do grau:
O exercício quer saber a probabilidade dessa equação ter raízes reais.

Bom, pela fórmula de Bhaskara (lá da escolinha...), sabemos que a solução dessa equação do grau é dada por:
Para essa equação possuir raízes reais, devemos ter , ou seja:
Ou seja:
Portanto, o que realmente estamos querendo saber é a probabilidade de termos .
Passo 2
Beleza, já conseguimos traduzir esse problema pra linguagem de probabilidade, mas como é que calculamos ?

Essa pergunta é bem difícil, mas o bizu é lembrar que em distribuição uniforme podemos calcular probabilidade usando a ideia de razão de áreas ocupadas pelos pontos.
Tipo assim, como e estão em , pensando no plano cartesiano, os possíveis pares formam um quadrado. Esse é o nosso espaço amostral!
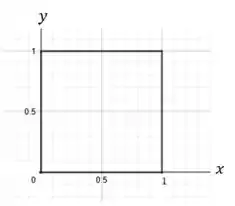
Beleza! Mas também temos a restrição pela equação:
Os pares de pontos que obedecem a essa equação, serão os pontos abaixo da curva:
Que é uma hipérbole, com variando de a ! Vamos plotar ela no gráfico também:
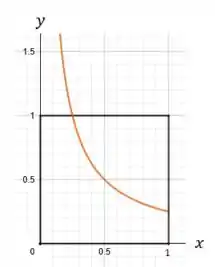
Muito bom! Agora chegamos que temos tanto os pontos favoráveis como o espaço amostral, pela definição de probabilidade, podemos dizer que:
Onde:
é a área abaixo da curva da hipérbole e dentro do quadrado de .
é a área do quadrado que representa o espaço amostral dos pares .

Passo 3
Massa! Bora calcular essas áreas então!
A área do quadrado é bem simples, né?!
Já a dá um trabalhinho a mais! Vamos dividi-la em duas partes:
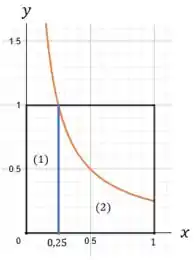
Daí:
A área é simplesmente a área do retângulo formado na região .
Lembrando que o ponto de interseção da hipérbole com a reta , pode ser encontrado fazendo:
Portanto, temos:
Já a área da região precisa ser calculada com o auxílio da integral. Na prática, essa região é composta pelos pontos abaixo da curva entre os pontos .
Assim, temos:
Excelente! Logo:
Agora é só correr pro abraço, pois:
Prontinho galera! Mais uma questão finalizada.
Bem legal essa ideia da probabilidade como área né?!
Valeu pessoal, até a próxima 😊
Resposta
Letra C: