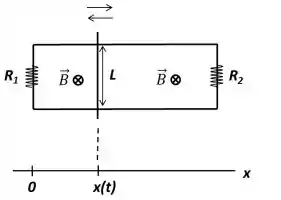
Uma barra condutora de comprimento pode deslizar sem atrito sobre trilhos horizontais condutores. A barra e os trilhos possuem resistência desprezível, mas há resistências e nos lados do circuito paralelos à barra. Em toda a região, atua um campo magnético uniforme e constante de módulo dirigido para dentro da folha de papel. Considere que a barra seja movimentada por um agente externo e que sua posição em função do tempo seja dada por [unidades SI].
a) (1,0) Para o instante , calcule a corrente total ao longo da barra e indique seu sentido (para cima ou para baixo).
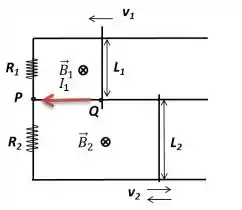
De acordo com a nova figura, um novo circuito é montado com as mesmas resistências e , com trilhos horizontais sem atrito e duas barras condutoras de comprimentos e que podem ser movimentadas de modo independente. Trilhos e barras possuem resistência nula. Em cada malha, atua um campo magnético uniforme diferente, de módulos e , dirigidos para dentro da folha.
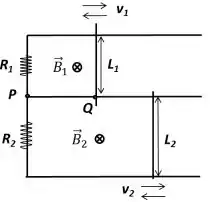
b) (1,0) Considerando (barra 2 imóvel) e , calcule a velocidade constante que a barra 1 deve possuir e indique seu sentido (para direita ou para esquerda) para que a corrente no trecho PQ possua valor e sentido de Q para P.
c) (1,0) Considerando e , calcule o módulo da razão entre as velocidades das barras (ambas constantes) para que a corrente total no trecho PQ seja nula. Para esta condição, responda, também, se as velocidades devem ter o mesmo sentido ou sentidos contrários.
Passo 1
Cara... Veja bem... Temos nesse problema duas espiras retangulares separadas pela barra (espira esquerda e direita):
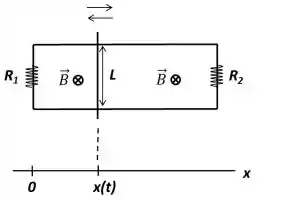
Só que aí de repente a Barra começa a se locomover com velocidade para um dos sentidos (direita ou esquerda). De qualquer modo, as áreas das duas espiras vão mudar de modo a gerar uma variação no fluxo do campo elétrico que atravessa as duas espiras (por um lado a quantidade de campo elétrico atravessando aumenta e por outro diminui). De acordo com a Lei de Faraday, essa variação de fluxo magnético produz sobre as espiras.
Bem... A pode então ser encontrada fazendo...
Daí... Dada a sobre uma espira (digamos a da espira esquerda), basta dividir essa pela resistência para se obtiver a corrente :
“AHHH! Mas a gente vai ter que necessariamente determinar o fluxo primeiro?”
A ótima notícia que eu tenho para te dar é que não! Existe um Bizu para se obter essa ! Vamos ver isso na prática?
Passo 2
POW! A forma de se calcular sem ter que necessariamente calcular um fluxo, é se lembrando de que para uma espira retangular podemos sempre usar a fórmula prontinha...
Veja que já temos o valor de e . Ta faltando só encontrar mesmo a velocidade nas duas espiras!
O problema nos informou que a espira tem posição em função do tempo dada por...
ORA! A velocidade é a derivada da posição! Então...
Então... A velocidade da barra então no tempo ...
OPA!!! Velocidade positiva? Isso só pode significar que a barra está se movendo para a direita!
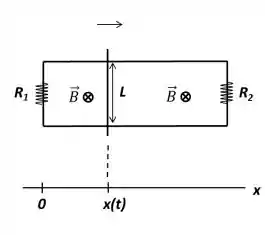
Então, as duas espiras, direita e esquerda vão possuir a mesma (o motivo é porque elas estão em série)...
Então com isso podemos buscar a corrente em cada espira e depois somar para saber a corrente total que passa no trilho. Bora?
Passo 3
CALCULANDO A CORRENTE CIRCULANDO NA ESPIRA ESQUERDA:
A espira a esquerda tem , então...
Agora, a corrente tem que estar girando no sentido anti-horário nessa bobina:
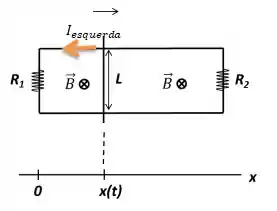
Agora, porque que isso está acontecendo?
Pela Lei de Lenz! A Lei de Lenz nos fala que a corrente que surge sempre deve possuir um campo magnético induzido de modo a se opor a variação do fluxo do campo externo.
Então veja bem, fixando a atenção na espira esquerda, veja que a medida que a barra vai para a esquerda terá mais campo magnético entrando na espira. Então, pela Lei de Lenz, o campo da corrente tem que ter sentido oposto, ou seja, saindo da tela. E pela Regra da mão direita isso só acontece quando a corrente gira no sentido anti-horário, saca?
CALCULANDO A CORRENTE CIRCULANDO NA ESPIRA DIREITA:
A espira a direita tem , então...
Agora, a corrente tem que estar girando no sentido horário nessa bobina:
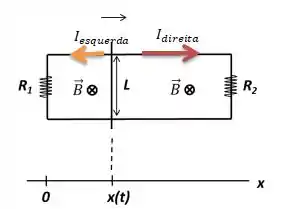
E o motivo é que desse lado, a quantidade de campo externo entrando se reduz, então a corrente pela Lei de Lenz tem que girar no sentido horário de modo a produzir um campo entrando “ajudando” o campo externo a manter o fluxo de campo saindo, saca?
RESUMINDO
Então, a corrente que passa pelo trilho será...
E ela deve estar subindo no trilho para se dividir nas correntes e .
Passo 4
Bem... Nesse problema daqui de modo análogo ao anterior vamos agora trabalhar com esse circuito aqui...
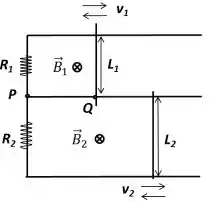
Considerando a espira parada, queremos saber qual deve ser a velocidade na barra para a corrente indo de para na espira de cima.
Ora... Como vimos no passo anterior, para uma espira retangular, a induzida é dada por...
E a corrente girando na espira então é dada por...
Isolando ...
A corrente vale e os outros caras já forma dados no problema, então...
Agora surge a pergunta, para que lado o trilho está caminhando?
Passo 5
POW! Sabemos que a corrente que gira na espira de modo a atravessar de para . Isso significa que a corrente está gerando um fluxo induzido de campo magnético que está entrando na região de modo a ajudar o campo externo...
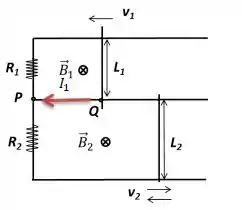
No passo , vimos que isso só acontece quando o fluxo externo de está diminuindo e o então o fluxo produzido pela corrente tende a ajudar a manter o externo intacto. Para o fluxo estar diminuindo, concluímos que a barra tem que movimentar para a esquerda.
Passo 6
POW! Imagine você que existe ainda uma corrente para a esquerda em , causada pela variação da barra ...
Para zerarmos essa corrente temos que passar outra corrente de mesmo módulo no sentido contrário...
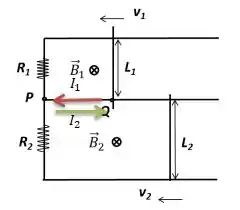
O que só acontece se ambas as barras se movimentarem no mesmo sentido, já que ambos os campos são para dentro.
Agora, como a gente encontra a razão ?
Passo 7
Bem... Sabemos que ambas correntes ( e ) devem ser iguais...
A corrente ...
A por sua vez pode ser determinada por...
Então...
Resposta
Letra A:
Letra B:
Letra C: