Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RL

Ver Teoria
Exercício 612345789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354

Enunciado

Na figura, a chave S ficou fechada por um tempo muito longo.

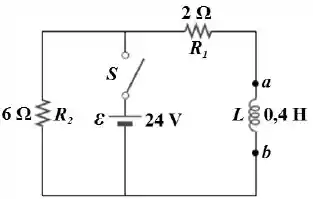
a ) Quais são as correntes através de R 1 e R 2 ?

b ) Qual é a energia armazenada no indutor?

A chave é então aberta em t = 0 .

c ) Escreva a expressão da corrente através do indutor em função do tempo;

d ) Calcule a ddp inicial t = 0 através do indutor;

Passo 1

a ) Quais são as correntes através de R 1 e R 2 ?

Depois que a chave fica fechada por muito tempo t → ∞ , a corrente no indutor tende a ficar constante o indutor passa a se comportar como um “pedaço de fio” comum. Então não devemos leva-lo em consideração nessa situação. Assim o nosso circuito vai ser as duas resistências em paralelo!

Logo:

i 1 = ε R 1 = 24 2 = 12   A

i 2 = ε R 2 = 24 6 = 4   A

Passo 2

b ) Qual é a energia armazenada no indutor?

A energia armazenada em um indutor é dada por:

U = L i 1 2 2

Substituindo os valores:

U = 0,4 2   12 2 = 28,8   J

Passo 3

c ) Escreva a expressão da corrente através do indutor em função do tempo;

Aplicando Lei das malhas na malha total de fora (excluindo o fio que contém a bateria), temos:

- i 1 . R 1 - L . d i 1 d t - i 2 R 2 = 0

Nesse caso, temos i 1 = i 2 . Logo:

i 1 . R 1 + L . d i 1 d t + i 1 R 2 = 0

A solução dessa equação é:

i 1 t = i 0 e - ( R 1 + R 2 ) t L

Onde L R 1 + R 2 pode ser substituído por τ L , que a denominada constante de tempo indutiva. Essa equação nos dá corrente no circuito!

Como após desligar a chave, a única fonte de d.d.p. é o indutor (por que ele tem uma energia armazenada) a corrente no instante t = 0 vai ser a corrente no indutor que vimos no passo anterior

i 0 = 12 A

Assim substituindo todos os nossos valores

i 1 t = 12 e - 20 t

Passo 4

d ) Calcule a ddp inicial t = 0 através do indutor;

Temos que a ddp no indutor é dada por:

V L = L d i 1 d t = L d d t i 0 e - ( R 1 + R 2 ) t L = - L R 1 + R 2 L i 0 e - ( R 1 + R 2 ) t L

V L = - R 1 + R 2 i 0 e - ( R 1 + R 2 ) t L  

Quando t = 0 :

L . d i 1 d t = - R 1 + R 2 i 0 = - 2 + 6 12

V L = - 96   V

Resposta

a )

i 1 = 12   A

i 2 = 4   A

b )

U = 28,8   J

c )

i 1 t = i 0 e - ( R 1 + R 2 ) t L

d )

- 96   V

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm