Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RL

Ver Teoria
Exercício 141234567891011121315161718192021222324252627282930313233343536373839404142434445464748495051525354

Enunciado

Circuitos RL

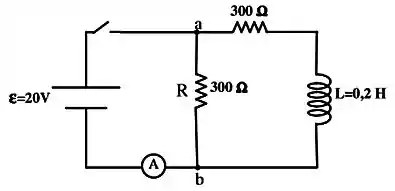
No circuito abaixo, determine o valor indicado no amperímetro, justificando sua resposta,

  1. No momento em que ligamos a chave.
  2. Muito tempo depois da chave ser ligada.

    3. A chave é novamente aberta.

  3. Neste instante, pelo caminho da resistência R , quanto vale V a - V b ?

Passo 1

É importante observar a expressão “no momento em que ligamos a chave” porque a questão está exatamente aí. Antes da chave fechar a corrente no indutor era i L = 0 . O indutor impede que tenha variação instantânea da corrente, assim, no momento em que ligamos a chave, a corrente no indutor continua i L = 0 .

Logo, a corrente marcada no amperímetro é apenas a corrente passada no R (em paralelo com o indutor).

ε = R i

20 = 300 i

i = 0,067   A

Passo 2

A expressão agora mudou para “muito tempo depois da chave ser ligada”. A consequência disso é que, agora, o indutor comporta-se como um fio. Logo, temos um circuito simples.

Como são duas resistências de 300 Ω , a resistência equivalente vale 150 Ω .

R e q = 300 ∙ 300 300 + 300 = 150 Ω

E então, calculamos o valor da corrente:

ε = R i

20 = 150 i

i = 0,134   A

Passo 3

A ddp entre os pontos a e b continua valendo 20 V .

Resposta

  1. i = 0,067   A
  2. i = 0,134   A
  3. V a - V b = 20 V

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm