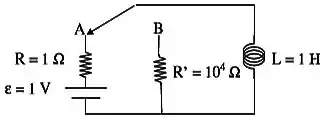
No circuito abaixo, a chave ficou conectada por um longo tempo ao ponto . Considere o momento em que a chave é comutada para o ponto . Calcule:
- A corrente que passa pelo indutor no momento em que a chave é conectada ao ponto .
- A diferença de potencial sobre o resistor no momento em que a chave é conectada ao ponto .
- A energia dissipada no resistor no intervalo de tempo entre e .
Passo 1
Bem, é pra considerar no momento em que a chave é conectada ao ponto . Isto significa que a corrente é a mesma da situação anterior (chave conectada em ) devido a presença do indutor que inibe a variação instantânea da corrente.
Então, calculamos a situação da chave em .
Passo 2
A corrente que passa em é de , logo a ddp é:
Passo 3
Consideramos, aqui, a constante de tempo de dacaimento da corrente.
Temos, então, que
Então, para , a corrente já é nula e toda a energia acumulada no indutor foi perdida por efeito Joule no resistor.
Sendo assim,