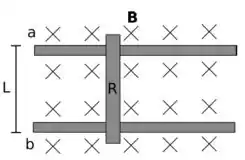
1) Na figura ao lado, a barra vertical tem massa , comprimento e resistência entre suas extremidades. Os trilhos são horizontais, sem atrito e têm resistências desprezíveis. A distância entre os trilhos também é . Uma bateria ideal, com , está conectada entre os pontos e de tal forma que a corrente na barra é para baixo. A barra é liberada a partir do repouso em .
a) Deduza uma expressão para a força horizontal na barra como função da velocidade e das demais grandezas fornecidas.
b) Mostre que a velocidade da barra se aproxima de um valor máximo após um longo tempo, e determine uma expressão para esta velocidade.
c) Qual é a corrente quando a barra está se movendo com a velocidade máxima? Justifique todos os itens.
Passo 1
E aiii... nós de novo!
Na letra b vamos mostar que a velocidade se aproxima de um valor máximo. Maas antes disso precisamos achar uma expressão pra velocidade, né?
Vamos usar a segunda lei de Newton:
Vamos pegar a força que achamos na letra a:
E resgatar uma lembrancinha de que a aceleração é a derivada da velocidade:
Para a letra c, vamos pegar a corrente que também achamos na letra a:
Passo 2
Igualando as forças, temos:
E como a aceleração é a derivada da velocidade:
Separando as variáveis:
Integrando ambos os lados:
Passo 3
Agora que achamos uma expressão pra velocidade, vamos fazer esse tempo ser beeem grande. Isso lembra limite tendendo a infinite, não é?
Repara que vai pra que é aproximadamente zero.
Passo 4
Pra resolver a letra c, só precisamos jogar essa velocidade limite na expressão da corrente:
Acabamos mais uma, heim!? Partiu pra próxima.
Resposta
a) e demonstração nos passos.
b)