Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RL

Ver Teoria
Exercício 221234567891011121314151617181920212324252627282930313233343536373839404142434445464748495051525354

Enunciado

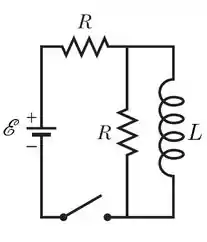
O circuito ilustrado abaixo contém uma fonte de força eletromotriz ε = 18   V , dois resistores de mesma resistência R = 3 Ω e um indutor de indutância L = 2 m H . No instante de tempo t = 0 a chave é fechada. Assinale a alternativa que indica a corrente na fonte em t = 0 , i ( 0 ) , e para t = ∞ :

(a) i 0 = 2 A e i ∞ = 6 A

(b) i 0 = 0 A e i ∞ = 1,5 A

(c) i 0 = 6 A e i ∞ = 1,5 A

(d) i 0 = 3 A e i ∞ = 6 A

(e) i 0 = 1 A e i ∞ = 1 A

Passo 1

Primeiramente temos que relacionar as correntes e voltagens!

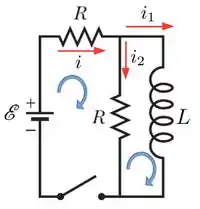
Olhando para o nó superior na figura, temos

i = i 1 + i 2

Olhando para a malha da esquerda temos

ε - R i - R i 2 = 0

E olhando para a malha da direita, temos

- L d i 1 d t + R i 2 = 0

Queremos olhar o comportamento da corrente i , mas antes temos que olhar para as outras correntes!

Passo 2

Vamos olhar para a corrente no indutor! A última equação envolve a derivada temporal da corrente i 1 dependendo da corrente i 2 . Podemos escrever i 2 como função de i 1 usando as duas primeiras equações

i = i 1 + i 2 ε - R i - R i 2 = 0 →   ε - R ( i 1 + i 2 ) - R i 2 = 0

R i 1 + 2 i 2 = ε

Isolando i 2

i 2 = ε 2 R - i 1 2

Assim a equação da malha da direita fica

- L d i 1 d t + R i 2 = 0 → - L d i 1 d t + R ε 2 R - i 1 2 = 0

d i 1 d t = ε 2 L - R 2 L i 1

E essa é a equação diferencial para a nossa corrente no indutor.

Resolver ela é moleza, basta fazer uma substituição α = ε / 2 L   - i 1 R / 2 L , e depois fazer a separação de variáveis. A solução será

i 1 t = ε R 1 - e - t 2 τ L + i 1 0 e - t 2 τ L

Como a chave antes de t = 0 estava aberta não havia corrente no indutor antes de fecharmos a chave, o que quer dizer que i 1 0 = 0

i 1 t = ε R 1 - e - t 2 τ L

Passo 3

Agora vamos olhar para o comportamento de i 1 e consequentemente o das correntes i 2 e i (a que nos interessa), já que

i 2 = ε 2 R - i 1 2

i = i 1 + i 2 = i 1 + ε 2 R - i 1 2 → i = ε 2 R + i 1 2

Assim que fechamos a chave ( t = 0 ), temos

i 1 ( 0 ) = 0

i 2 0 = ε 2 R - i 1 0 2 = ε 2 R = 18 2.3 = 3 A

i 0 = i 1 0 + i 2 0 = 0 + 3 = 3 A

Depois de passado um tempo muito longo, temos o limite t → ∞ e a exponencial na corrente i 1 vai pra 0 . Assim

i 1 ∞ = ε R = 18 3 = 6 A

i 2 ∞ = ε 2 R - i 1 ∞ 2 = 18 2.3 - 6 2 = 0 A

i ∞ = i 1 ∞ + i 2 ∞ = 6 + 0 = 6 A

Logo a corrente i na fonte em t = 0 é 3 A e em t → ∞ é 6 A .

Resposta

(d)

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm