Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RL

Ver Teoria
Exercício 431234567891011121314151617181920212223242526272829303132333435363738394041424445464748495051525354

Enunciado

Circuitos RL

No circuito abaixo a corrente inicial é nula. No instante inicial a chave S é fechada, neste instante determine:

  1. A corrente em todo o circuito.
  2. A diferença de potencial sobre o indutor.

    3. Passado um tempo muito longo após a chave S ser fechada, determine:

  3. A corrente em todo o circuito.
  4. A diferença de potencial sobre o indutor.

    5. A chave S então é aberta, neste instante, determine:

  5. A corrente em todo o circuito.
  6. A diferença de potencial sobre o indutor.

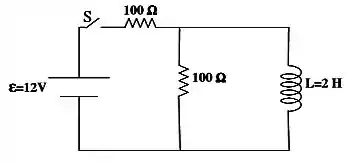
Passo 1

Primeira coisa a se observar: a questão pede no instante em que a chave é fechada. Ou seja, não passa corrente no indutor visto que ele não permite uma variação instantânea de corrente.

Torna-se um circuito simples, com R e q = 200   Ω e E = 12 V .

E = R i

12 = 200 i

i = 60   m A

Passo 2

Bem, o indutor está em paralelo com uma resistência de valor R = 100 Ω , então terá a mesma ddp deste resistor.

E = 100 ∙ 0,06

E = 6 V

Passo 3

Agora a questão diz que já passou muito tempo que a chave foi fechada. Ou seja, passa uma corrente estabilizada no condutor, como se ele se comportasse como um fio.

Neste caso, em que o indutor e o segundo resistor estão em paralelo, a corrente “escolhe” passar pelo indutor que se comporta apenas como um fio do que passar por um resistor que se comporta como um resistor. Então, temos corrente apenas no primeiro resistor.

E = R i

12 = 100 i

i = 120   m A

Passo 4

Podemos calcular a ddp de novo baseando-se no resistor em paralelo. Como não tem corrente passando pelo resistor, E = 0 V .

Passo 5

Como visto cá em cima, o indutor não permite uma variação instantânea da corrente. Então, no instante em que a chave é reaberta, a corrente permace a mesma da situação anterior: i = 120   m A .

Passo 6

E mais uma vez, veremos a ddp no indutor calculando a ddp no resistor em paralelo. Como toda a corrente passa através do indutor, a corrente através do resistor em paralelo será nula e, consequentemente, a ddp através do mesmo também será nula, logo:

E = 0 V

Resposta

  1. i = 60   m A
  2. E = 6 V
  3. i = 120   m A
  4. E = 0 V
  5. i = 120   m A
  6. E = 0 V

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm