Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RL

Ver Teoria
Exercício 512346789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354

Enunciado

No circuito da figura abaixo, a chave S ficou na posição A por um tempo muito longo.

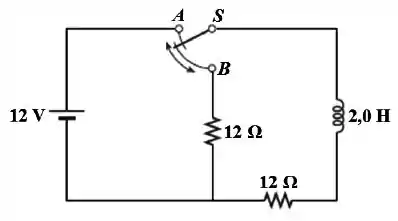
a ) Nesta condição, qual é a corrente no circuito?

Agora, S é subitamente movida de A para B em t = 0 .

b ) Calcule a d d p inicial através do indutor e através de cada resistor.

c ) Calcule a energia magnética inicial armazenada no indutor.

d ) Calcule a energia total dissipada nos resistores.

Passo 1

a ) Qual é a corrente no circuito?

Em um circuito R L , quando o indutor está conectado à fonte, a corrente no circuito obedece à função:

i = ε R . 1 - e - R t L

Depois que a chave fica na posição A por muito tempo t → ∞ , a corrente no indutor tende a ficar constante o indutor passa a se comportar como um “pedaço de fio” comum. Então não devemos leva-lo em consideração nessa situação.

Logo:

i = ε R = 12 12

i = 1   A

Passo 2

b ) Calcule a d d p inicial através do indutor e através de cada resistor.

Quando a chave é movida para a posição B , o circuito passa a ser formado somente pelo indutor e pelos resistores.

Nessa situação, a corrente no circuito é dada por:

i = ε R e q . e - R e q t L

A partir daqui já podemos começar a brincar.

A d d p nos resistores é dada por:

V R = R i = R ε R e q . e - R e q t L

E a d d p no indutor é dada por:

V L = - L d i d t = ε . e - R e q t L

Em t = 0 , teremos:

V R = R ε R e q = 12 × 12 12 + 12

V R = 6   V

V L = ε = 12   V

Passo 3

c ) Calcule a energia magnética inicial armazenada no indutor.

A energia magnética é dada por:

U L = L i 2 2

A corrente inicial do circuito é dada por:

i = ε R e q = 12 12 + 12

i = 0,5   A

Logo:

U L = 2 × 0,5 2 2

U L = 0,25   J

Passo 4

d ) Calcule a energia total dissipada nos resistores.

Toda a energia armazenada no indutor será dissipada nos resistores, logo, a energia total dissipada nos resistores será:

U R = U L

U R = 0,25   J

Resposta

a )

i = 1   A

b )

V R = 6   V

V L = 12   V

c )

U L = 0,25   J

d )

U R = 0,25   J

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm