As duas chaves do circuito que segue são fechadas em . Determine , e para .
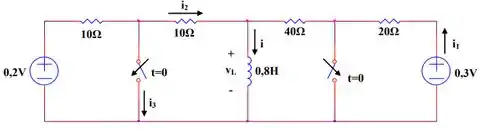
Passo 1
Antes de , com o indutor em curto, temos que . Assim, a corrente para é dada por:
Além disso, calculamos para pela lei das malhas:
E também para :
Por fim, calculamos para como:
Passo 2
Após o fechamento das chaves, o indutor fica em paralelo com as resistências de e e as fontes deixam de alimentar o indutor, como na figura abaixo.
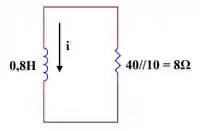
Assim, para :
E o valor de será:
Passo 3
Para obter a corrente para , vamos olhar para a figura abaixo.
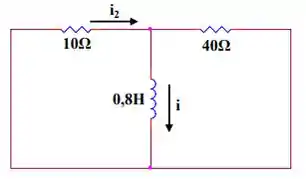
Temos que:
onde chamamos de a corrente que passa pelo resistor de .
Sabemos que a tensão nos dois resistores é a mesma. Logo:
Substituindo:
Resposta
Para :
Exercícios de Livros Relacionados
Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm