Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos RL

Ver Teoria
Exercício 301234567891011121314151617181920212223242526272829313233343536373839404142434445464748495051525354

Enunciado

Para a solução desse exercício, considere R 1 , R 2 , L e E como dados do problema.

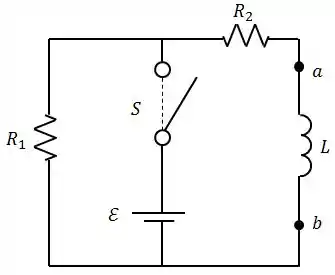
a A chave S esteve fechada até que as condições estacionárias foram atingidas, Calcule a corrente no circuito nessa situação.

b Em seguida abre-se a chave. Determine a f e m através do indutor imediatamente após a abertura de S .

Passo 1

a A chave S esteve fechada até que as condições estacionárias foram atingidas, Calcule a corrente no circuito nessa situação.

A fonte E é quem gera a corrente no circuito, então vamos analisar duas malhas aqui, beleza?

A primeira malha é formada pela fonte E e pelo resistor R 1 , enquanto a segunda malha é formada pela fonte E , pelo resistor R 2 e pelo indutor L .

Vamos percorrer as duas malhas para encontrar expressões para as correntes no circuito.

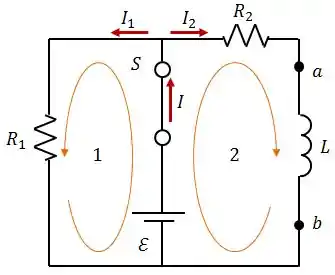
Utilizando a Lei das Malhas de Kirchhoff, teremos:

  • Malha 1:

    • E - I 1 R 1 = 0

    I 1 = E R 1

  • Malha 2:

Essa malha corresponde a um circuito R L , onde a corrente varia de acordo com a seguinte equação:

I 2 t = E R 2 1 - e - R 2 t L

Como estamos considerando que se passou tempo suficiente para que a situação estacionária fosse atingida, podemos dizer que:

t → ∞

I 2 = E R 2

Assim, a corrente que passa pela fonte será:

I = I 1 + I 2

I = E R 1 + E R 2

I = E R 1 + R 2 R 1 R 2

Passo 2

b Em seguida abre-se a chave. Determine a f e m através do indutor imediatamente após a abertura de S .

Assim que abrimos o circuito, a fonte para de abastecer o circuito e a corrente no indutor passa a variar de acordo com a equação:

I 2 t = I m á x e - R 1 + R 2 t L

Isso porque, agora, o circuito é composto pelas resistências R 1 e R 2 associadas em série, além do indutor.

No entanto, vimos no Passo 1 que a corrente máxima no indutor era:

I m á x = E R 2

Dessa forma:

I 2 t = E R 2 e - R 1 + R 2 t L

Passo 3

A f e m no indutor é dada por:

E L = - L d I 2 d t

Derivando a expressão que encontramos no Passo 2, teremos:

E L = - L E [ - R 1 + R 2 ] R 2 L e - R 1 + R 2 t L

E L = E R 1 + R 2 R 2 e - R 1 + R 2 t L

Imediatamente após abrir a chave S , considerando t = 0 na equação acima, teremos:

E L = E R 1 + R 2 R 2 e 0

E L = E R 1 + R 2 R 2

Resposta

a

I = E R 1 + R 2 R 1 R 2

b

E L = E R 1 + R 2 R 2

Exercícios de Livros Relacionados

Quanto tempo é necessário, depois que a fonta é removida, para que a diferença de potencial entre os terminais do resistor de um circuito RL com L = 2,00H e R = 3,00Ω diminua para 10,0 % do valor inic
Um gerador de frequência ajustável é ligado em série com um indutor L = 2,50m H e um capacitor C = 3,00μ F . Para que frequência o gerador uma corrente com a maior amplitude possível no circuito?
A força eletromotriz da fonte do circuito da Fig. 30-16 varia com o tempo de tal forma que a corrente é dada por i t = 3,0 + 5,0 t , onde i está em ampères e t em segundos. Suponha que R = 4,0Ω e L =
Na Fig. 30-70, depois que a chave S é fechada no instante t = 0 , a força eletromotriz da fonte é ajustada automaticamente para manter uma corrente constante i passando pela chave. (a) Determine a cor
Na figura 30-73a, a chave S permaneceu na posição A por um tempo suficiente para que a corrente no indutor de indutância L 1 = 5,00m H e o resistor de resistência R 1 = 25,0Ω se estabilizasse. Da mesm