No circuito da figura ao lado a chave é fechada no instante .
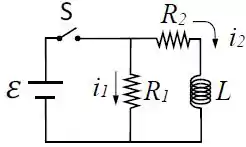
Determine, em função da tensão da fonte, da indutância e das resistências e :
As correntes e , presentes no circuito, quando e quando .
Após um tempo muito longo, a chave é reaberta. Determine a potência que é dissipada nos resistores em função do tempo.
Determine a energia magnética do circuito, em função do tempo, a partir da reabertura da chave .
Passo 1
As correntes e , presentes no circuito, quando e quando .
A corrente no ramo do indutor varia da seguinte forma:
Assim, quando e quando , teremos:
Utilizando a Lei das Malhas na malha que contém a fonte e a resistência , teremos:
Nesse caso, a corrente não varia com o tempo, logo:
Passo 2
Após um tempo muito longo, a chave é reaberta. Determine a potência que é dissipada nos resistores em função do tempo.
Quando a chave é aberta, a corrente no circuito decai com o tempo de acordo com a equação:
Obs.: O termo corresponde à corrente máxima que passa pelo indutor no momento em que a chave é aberta.
Agora o circuito conta com duas resistências, logo:
Assim, a corrente decai com o tempo de acordo com a função:
Finalmente, a potência dissipada no circuito é dada por:
Passo 3
Determine a energia magnética do circuito, em função do tempo, a partir da reabertura da chave .
A energia magnética do circuito é dada por:
Substituindo a função da corrente, teremos:
Resposta