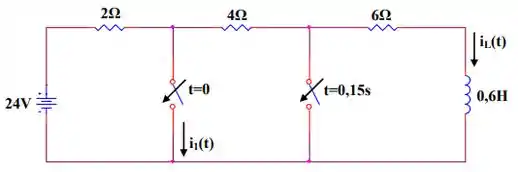
A chave da esquerda no circuito que segue é fechada em
(a) Determinar e para .
(b) A chave do lado direito é fechada em . Determine e para
Passo 1
(a) Determinar e para .
Para , temos que:
Além disso, o indutor está em curto e os resistores , e estão em série. Logo,
Para , com a chave da esquerda fechada, temos que:
onde o valor de é dado pela soma das resistências e , já que estes resistores estão em série. Temos:
Já para calcular , utilizamos a lei das correntes:
Passo 2
(b) Determine e para
Nesse caso, temos que:
e
Resposta
(a) e
(b) e