UFSJ; Física 3; AV3 – 2ª CH – 2018.2; questão 3d
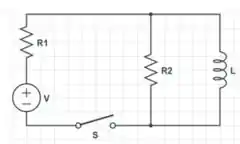
O circuito abaixo ficou durante um tempo longo com a chave fechada. No instante , a chave é aberta.
d) Determine a energia total dissipada por efeito Joule no resistor para . Compare com o que foi encontrado no item (b).
Passo 1
E aí pessoal, tudo bão por aí???
Hoje nós vamos destruir essa questão! Vem comigooo!
Seguinte galerinha, nós temos um circuito que passou bastante tempo fechado e no momento , a chave foi aberta e a partir desse instante a chave se manteve em regime estacionário. O nosso circuitinho está representado nessa imagem abaixo.
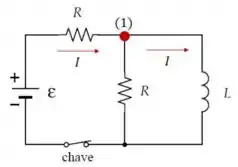
O problema aqui é determinar a energia total dissipada por efeito Joule no resistor no momento !!
Passo 2
Aqui basta lembrar que a energia armazenada no indutor é dada pela seguinte equação, olha só:
O enunciado nos pede que o cálculo da energia seja feita no momento , ou seja, a corrente elétrica é a própria corrente no indutor, , então temos que a energia no indutor é:
Nesse momento, o indutor possui corrente máxima, logo, energia máxima também! Porém, quando a chave é aberta, a corrente diminui e, consequentemente, a energia também diminui. Isso acontece porque a energia fornecida pelo indutor acaba sendo dissipada pelo resistor. Portantooo, a energia total dissipada é a própria energia do indutor!!
Prontinho, conseguimos uuhhhh!
Curtiu a resolução? Responde Aí!!