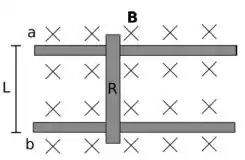
1) Na figura ao lado, a barra vertical tem massa , comprimento e resistência entre suas extremidades. Os trilhos são horizontais, sem atrito e têm resistências desprezíveis. A distância entre os trilhos também é . Uma bateria ideal, com , está conectada entre os pontos e de tal forma que a corrente na barra é para baixo. A barra é liberada a partir do repouso em .
a) Deduza uma expressão para a força horizontal na barra como função da velocidade e das demais grandezas fornecidas.
b) Mostre que a velocidade da barra se aproxima de um valor máximo após um longo tempo, e determine uma expressão para esta velocidade.
c) Qual é a corrente quando a barra está se movendo com a velocidade máxima? Justifique todos os itens.
Passo 1
Falaaa, galerinha. Tudo bem??
Entendo um pouco melhor o que está acontecendo na questão...
Temos uma barra que vai deslizar sobre o trilho. Repara que já temos uma bateria, daí já temos uma corrente passando pela barra (para baixo, dado no enunciado). Como já tem essa bateria, então a barra vai entrar em movimento com uma velocidade.
Por outro lado, conforme a barra vai se movendo, uma corrente induzida (induzida) vai ocorrer no sentido contrário.
Na letra a, vamos calcular a força horizontal. Não tem nenhuma outra força além da magnética no sistema. Ela é dada pelo produto vetorial:
Também vamos precisar da relação:
Para a induzida temos:
Passo 2
Primeira coisa que vamos fazer é achar a corrente líquida no sistema.
Como tem a da bateria num sentido e a induzida no sentido contrário:
Substituindo a induzida:
Passo 3
Resolvendo o produto vetorial da força magnética, ficamos com (usando a regra da mão direita):
Repara que , que é a barra, e , que é o campo magnético entrando na folha, formam o ângulo de 90°, então . Daí
Substituindo a corrente que achamos no passo anterior:
Essa é a força que atua horizontalmente na barra.
Acabamos essa. Bora pra próxima...