Para o circuito ilustrado na figura, as resistências dos indutores são desprezíveis e o interruptor está aberto por um tempo muito longo.
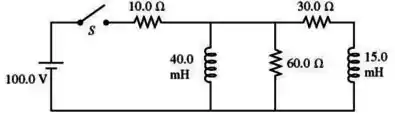
No instante em que se fecha o interruptor, qual é a corrente através da resistência de ?
No instante em que se fecha o interruptor, qual é a diferença de potencial do indutor de ?
A chave é fechada por um tempo muito longo, qual é a diferença de potencial através do resistor de ?
Passo 1
No instante em que se fecha o interruptor, qual é a corrente através da resistência de ?
Pela fórmula da variação da corrente em circuito RL, podemos ver que a corrente inicial através dos indutores é nula, isso porque os indutores irão se opor à corrente!
Para
Portanto, para analisar a corrente no resistor de vamos aplicar a lei das malhas à malha composta pela fonte de , o resistor de e o resistor de .
Como a corrente através dos indutores é inicialmente nula, a corrente que passa pelo resistor de é a mesma que passa pelo resistor de . Logo:
Passo 2
No instante em que se fecha o interruptor, qual é a diferença de potencial do indutor de ?
Vimos no Passo 1 que no instante inicial a corrente é nula através dos indutores. Assim, inicialmente não haverá corrente passando através do resistor de .
Dessa forma, aplicando a lei das malhas ao circuito formado pela fonte de , o resistor de , o resistor de e o indutor de , teremos:
Passo 3
A chave é fechada por um tempo muito longo, qual é a diferença de potencial através do resistor de ?
Depois de um longo tempo , temos que a corrente vale:
E toda a corrente do circuito vai passar pelo indutor de , que não apresenta nenhuma resistência.
Dessa forma, como nenhuma corrente passa pelo resistor de , a ddp através do mesmo será:
Resposta