UFSJ; Física 3; AV3 – 2ª CH – 2018.2; questão 3c
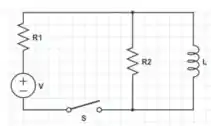
O circuito abaixo ficou durante um tempo longo com a chave fechada. No instante , a chave é aberta.
c) Obtenha a equação diferencial para a corrente através do indutor para e determine a sua solução.
Passo 1
E aí pessoal, tudo bão por aí???
Hoje nós vamos destruir essa questão! Vem comigooo!
Seguinte galerinha, nós temos um circuito que passou bastante tempo fechado e no momento , a chave foi aberta e a partir desse instante a chave se manteve em regime estacionário. O nosso circuitinho está representado nessa imagem abaixo.
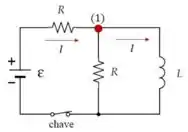
O problema aqui é determinar a equação diferencial para a corrente através do indutor para !!
Passo 2
O macete para conseguirmos resolver essa questãozita é entender que o enunciado nos pede a equação diferencial para a corrente através do indutor, ou seja, isso deve respeitar a condição inicial de , além disso, no momento a chave já estava aberta, portanto, a corrente já deixou de passar pelo indutor e está se dirigindo para a resistência, assim como podemos ver na imagem abaixo.
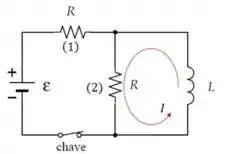
Você lembra que a soma das ddps de qualquer malha deve ser nula??
Passo 3
E agora a nossa missão é resolver essa equação diferencia!!
Como se trata de uma EDO de primeira ordem separável, vamos usar a estratégia de separar hahaha!
Primeiro passo é colocar cada um pro seu lado e passar a danada da integral!
Integrando, teremos:
Lembrando que a constante tempo indutiva é dada por:
Então, podemos substituir em .
E pra facilitar, vamos dar aquela simplificada!!
Prontinho, conseguimos uuhhhh!
Curtiu a resolução? Responde Aí!!