TAREFA da aula- 4 - Probabilidade e Estatística – Questão 1
A tabela abaixo corresponde à análise descritiva das alturas dos alunos matriculados na disciplina PROBEST-2013-2 turma 3VB.
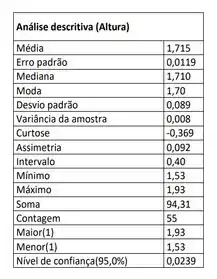
Usando os dados apresentados, pede-se:
a) Se a probabilidade de um aluno de PROBEST faltar à aula é de 4% e supondo que os alunos faltem às aulas de maneira estatisticamente independente entre si e no tempo, qual a chance de, nessa turma, o professor não ter nenhum aluno presente em um determinado dia de aula? b) E de comparecer mais de 52 alunos?
Passo 1
a) Bom! Pela contagem que aparece na figura do enunciado, o total de alunos da turma é de
E a questão nos diz que a probabilidade de algum faltar é de .
Agora pena só! Se é a variável aleatória que representa o nº de alunos que faltam aula, então temos que...
Nesse primeiro item a gente tem que determinar a probabilidade de não ter nenhum aluno na turma.
Pois muito bem! Pra gente calcular a probabilidade do professor não ter aluno nenhum pra dar aula, temos que calcular , probabilidade dos alunos faltarem.
Só usar a função de probabilidade da Binomial.
Bem baixa essa probabilidade! Etaaa que só tem aluno dedicado nessa turma!
Passo 2
b) Agora, vamos ver a probabilidade de comparecem mais de alunos...
Bom! Nessa caso, temos que calcular a probabilidade de que faltem menos do que alunos. Ou seja, temos que calcular o seguinte...
Usando a função de probabilidade binomial, temos que vai valer...
Já vai ser igual à...
E por último vai valer...
Somando tudo, temos que...
Ou seja! é a probabilidade de comparecerem mais de 52 alunos.
Turma boa, essa aí, hein!?
Resposta
a)
b)