Distribuição Bernoulli e Binomial
Sabe-se que um famoso atleta olímpico de tiro com arco costuma acertar o alvo na mosca em cerca de oito em cada dez vezes sob algumas condições específicas. Em um grande torneio internacional, em que estas mesmas condições acontencem, o atleta precisa acertar pelo menos duas vezes na mosca, em três tentativas, para ir às finais.
- Sabendo que a acurácia dos tiros não se altera, proponha um modelo para a variável aleatória que representa o número de acertos na mosca e calcule a probabilidade do atleta ir às finais.
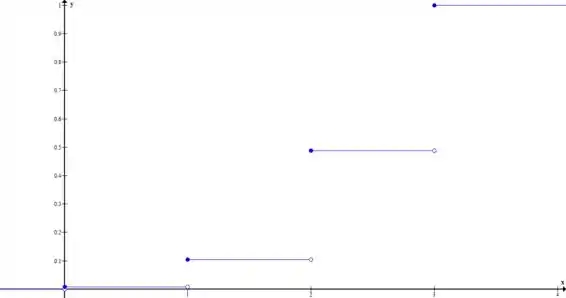
- Determine os valores da função de distribuição acumulada da variável aleatória definida no item anterior para valores do argumento pertencente aos intervalos , , , e . Forneça uma representação gráfica desta função.
Passo 1
(a)
Primeiro vamos propor um modelo para a v.a. .
Considerando como sucesso o atleta acertar na mosca, pelo enunciado a gente sabe que a probabilidade disso acontecer é.
Lembrando que o atleta só tem as opções: sucesso (acertar) ou fracasso (errar).
Como o cara vai ter 3 tentativas, .
Isso nos leva a uma distribuição Binomial, concorda ?
Passo 2
Agora a gente tem que calcular a probabilidade do cara ir as finais. Isso só acontece se ele acertar pelo menos 2 dentre as 3 tentativas.
Pela fórmula da Binomial.
Passo 3
Cálculos:
Logo:
Passo 4
(b)
Os valores possíves pra são: 0,1,2 e 3. Concorda ?
Primeiro então vamos determinar com qual probabilidade cada um desses valores possíveis acontecem, usando a fórmula da Binomial.
No item anterior a gente já calculou a prob. de e de .
Vou usar aquela tabelinha que a gente aprendeu.
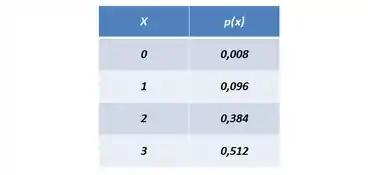
Passo 5
Pra terminar a gente tem que definir a nossa FDA. Lembrando que ela vai acumulando os valores anteriores, então, por exemplo:
Substituindo com os valores da tabela que a gente fez.
Passo 6
Fazer nosso gráfico da FDA.
