Distribuição Bernoulli e Binomial
Um supermercado faz a seguinte promoção: o cliente, ao passar pelo caixa, lança um dado honesto. Se sair face “6" ele ganha um desconto de 30% sobre o total de sua compra. Se sair face “5", o desconto é de 20%. Se sair face “4", o desconto é de 10% e, se sair faces “1", “2" ou “3", o desconto é de 5%. Seja a variável aleatória definida como o desconto concedido ao cliente na promoção. Pede-se:
- a função de probabilidade da variável aleatória ;
- o desconto médio concedido na promoção;
- a probabilidade de que num grupo de 5 clientes, pelo menos um obtenha um desconto maior do que 10%.
Passo 1
(a)
Temos:
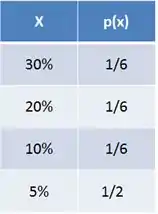
Pra fazer a função de probabilidade de a gente precisa fazer aquela nossa tabela, com os possíveis valores de e suas respectivas probabilidades.
A gente sabe de acordo com o enunciado que pode ser de 30%, 20%, 10% ou 5%.
Sendo que, como só temos 30% de desconto se sair 6 no dado, então:
Da mesma forma, temos:
Passo 2
Montamos nossa tabela.
Passo 3
(b)
Vamos calcular a esperança da v.a .
Passo 4
(c)
Primeiramente vamos ver qual a probabilidade de um cliente obter pelo menos um desconto maior que 10%.
Passo 5
Se a gente chamar de:
Temos que .
E a probabilidade de sucesso é
Podemos dizer então que:
Passo 6
Se a gente quer a probabilidade de pelo menos 1 dos clientes dentre os 5 conseguir o desconto, vamos ter:
Pela fórmula da Binomial,
Então: