Distribuição Bernoulli e Binomial
Retiram-se cartas, ao acaso e com reposição, de um baralho de cartas. Seja a variável aleatória definida como o número de reis na amostra.
- Obtenha a função de probabilidade de e faça um gráfico da sua função de distribuição acumulada.
- Obtenha a esperança e a variância de .
Passo 1
(a)
Vamos nomear nossa variável:
O baralho tem cartas no total, e dessas, são reis.. tá sabendo disso? Beleza.
Então qual a prob. de eu retirar um rei do baralho?
Vou repetir esse experimento de retirar uma carta do baralho vezes, com reposição e em todas as vezes a prob. de sucesso (sair um rei) é a mesma e igual a .
Isso significa que a nossa variável segue a distribuição Binomial.
Passo 2
Pra gente montar a função de probabilidade de a gente precisa dizer quais os possíveis resultados de e as suas respectivas probabilidades.
Primeiro então... vou retirar cartas do baralho, quais as possíveis quantidades de reis que eu vou poder ter?
Show?
E pra calcular a prob. de cada um a gente pode usar a fórmula da Binomial.
Passo 3
Aí temos:
Tá aí, todos os valores de e suas probabilidades.
Passo 4
Falta o gráfico da distribuição acumulada...
Como nosso é uma variável discreta nosso gráfico vai ser aquele que tem forma de degrau. Lembra?
Em cada valor possível de , que no caso são , você acumula o valor da probabilidade desse possível .
Fica assim:
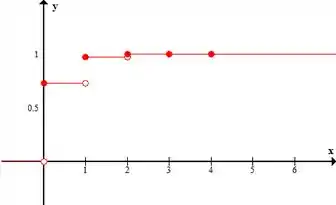
Cuidado que ali os valores ficam muito próximos, aí você tem que usar mais casas decimais pra poder diferenciar...
Passo 5
(b)
Como a gente já sabe que:
Fica fácil a gente calcular a esperança e a variância, é só usar as fórmulas: