UNICAMP – Cálculo 3 – 2020.2 – P1 – Discursiva
Considere a problema de valor inicial
Determine sua solução geral analiticamente. Justifique detalhadamente os passos de sua solução.
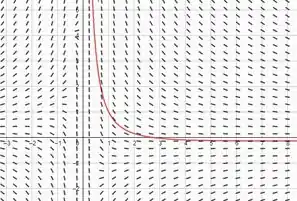
Resolva esse PVI no Mathematica. Exiba o gráfico da solução superposto ao campo de direções dessa equação diferencial.
Passo 1
Vamos começar resolver essa equação linear de primeira ordem não-homogênea dividindo toda a EDO por para ficar do jeitinho que a gente pode trabalhar com ela.
Sabemos então que e e com isso podemos resolver a nossa EDO.
Passo 2
Como já identificamos podemos usá-lo para achar :
Sabendo que:
Então vamos ter:
Resolvendo a integral:
Ou seja:
Passo 3
Agora o gráfico que o item fica da seguinte forma:
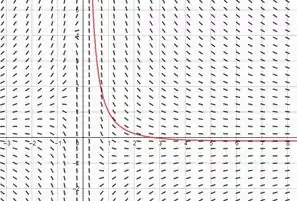
Resposta
Exercícios de Livros Relacionados
Ache a solução completa de cos x d y d x + y 2 = y s e n x Usando a solução de bernoulli 1 1 - nd u d x + P x u = Q x Sendo u= y 1 - n Com x no intervalo [ - π 2 , π 2 ]
Ache a solução completa de e x 2 d y d x + 2 x e x 2 y = x y ³ ³Usando a solução de bernoulli 1 1 - nd u d x + P x u = Q x Sendo u= y 1 - n
Em cada um dos problemas de 28 a 31, é dada uma equação de Bernoulli. Em cada caso, resolva-ausando a substituição mencionada no Problema 27(b)29 .y '=r y–k y 2 ,r0ek0 . Essa equação é importante em d
Em cada um dos problemas de 28 a 31, é dada uma equação de Bernoulli. Em cada caso, resolva-ausando a substituição mencionada no Problema 27(b)31 . d y d t=( Γc o s t+T ) y–y 3 , na qual Γ e T são con
Em cada um dos problemas de 28 a 31, é dada uma equação de Bernoulli. Em cada caso, resolva-ausando a substituição mencionada no Problema 27(b)30. y '=∊ y–σ y 3 ,∊0eσ0 ∊ ∊ . Essa equação aparece no es